Regular readers will remember Philippe Lemoine from my interview with him back in August. For those who missed it: Lemoine is a PhD candidate in philosophy at Cornell with a background in computer science. During the pandemic, he’s written several interesting articles, including a particularly good one titled ‘The Case Against Lockdowns’.
Lemoine’s latest article is a zinger. It begins with the puzzle of why the effective reproduction number often fluctuates wildly in the absence of changes in aggregate behaviour. Or put another way: why do infections sometimes start falling, or start rising, for no apparent reason?
I actually noted this puzzle myself in article back in March (which Lemoine kindly cites). Specifically, I noted that case numbers in South Dakota began falling rapidly in mid November, despite almost no government restrictions and little change in people’s overall mobility.
There are at least two existing explanations for this phenomenon. The first is seasonality: the effective reproduction number may partly depend on variables like temperature, humidity and UV light. Yet as Lemoine points out, there are many examples where case numbers changed suddenly that seasonality can’t explain (like South Dakota).
The second is viral evolution: the effective reproduction number may suddenly rise when a new, more-transmissible variant emerges (such as Delta or Omicron). Once again, however, case numbers have undergone dramatic changes in the absence of new variants. And while viral evolution can explain the rises, it has harder time explaining the falls.
Lemoine’s explanation is different: population structure. Traditional epidemiological models, he notes, assume the population is ‘quasi-homogenous’. This means that your chance of infecting someone of the same age who lives next door is the same as your chance of infecting someone of the same age who lives on the other side of the country.
Not very realistic, of course, but models have to make simplifying assumptions. How much does this one matter? It matters a lot, Lemoine argues.
Rather than assuming there’s one big quasi-homogenous population, imagine the population is divided into a large number of ‘subnetworks’. These could be based on location, age-group, behaviour or a combination of factors. For example, one subnetwork might be ‘school children and their parents in central London’.
Suppose that transmission occurs frequently within subnetworks but infrequently between them. So when a child within the school subnetwork catches the virus, it quickly spreads to other children and their parents. But what it doesn’t do is quickly spread to those outside the subnetwork.
Lemoine shows using simulations that, if you assume the population is structured in this way, the reproduction number can rise and fall without any changes in seasonality, viral evolution or aggregate behaviour. One of his simulations is show in the chart below.
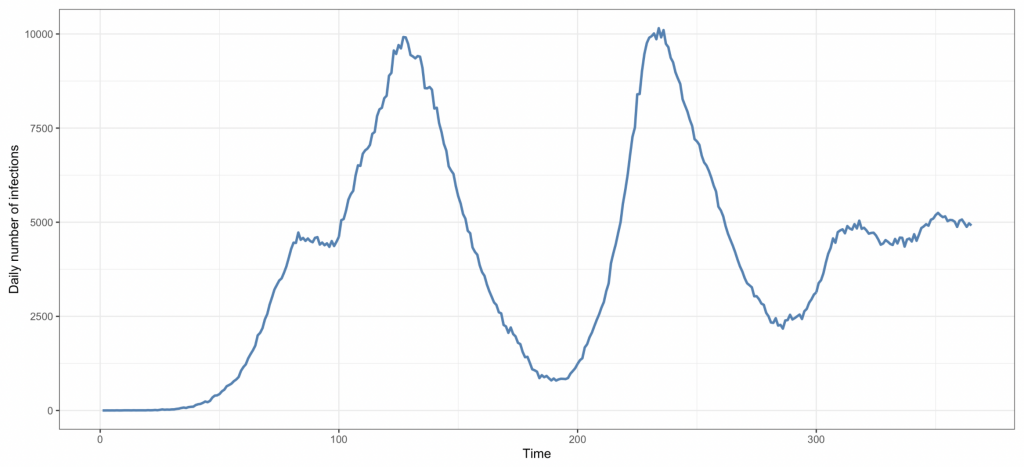
Compared to the giant single-peaked graphs produced by Imperial College researchers last year, it’s a much closer fit to empirical data. The idea is that once the virus exhausts all the susceptible people in one subnetwork, it takes time for other subnetworks to be seeded, and for new epidemics to emerge.
One interesting implication is that the overall epidemic ‘wave’ is actually the sum of waves in all the subnetworks where the virus is currently spreading. This means that several quantities we’ve been obsessing over, such as the effective reproduction number, might be “largely meaningless” at the aggregate level.
When infections start falling in a particular country, the Government often takes credit for having ‘gotten the R number below zero’. But if Lemoine is right, the R number may have fallen simply because the virus exhausted susceptible people in the subnetworks were it was recently spreading.
So governments may have been taking credit for fluctuations in the R number that were entirely independent of their policies.
Population structure is by no means inconsistent with other two explanations I mentioned earlier: seasonality and viral evolution. And although it’s hard to test empirically, the theory seems eminently plausible and worthy of consideration. Lemoine’s article is over 17,000 words, but it’s worth reading in full.











To join in with the discussion please make a donation to The Daily Sceptic.
Profanity and abuse will be removed and may lead to a permanent ban.