We have provided numerous explanations (see here, and here) and videos (see here and here) explaining why a vaccine that is actually merely a placebo will inevitably appear to have high efficacy if there is a time delay after vaccination during which the participant is classified as ‘unvaccinated’.
Some people have claimed that the examples – using hypothetical data – are unrealistic and that, with different assumptions about the underlying infection rate, the illusion would not happen. Not true.
This example simulates a vaccine roll-out and efficacy evaluation which is essentially how all the 2021 observational studies of the Covid vaccines were conducted.
Assumptions:
- The entire population starts week 1 as unvaccinated and by week 14 about 90% of the population has received a single jab (note that we start with a population of one million but the efficacy results are exactly same irrespective of the starting population).
- The vaccination rollout starts with 1% of the unvaccinated population vaccinated in week 1 and peaks at 35% in week 8 falling back to 10% in each of the last three weeks.
- There is a constant weekly infection rate throughout the period (in the example below it is 2% but, as the video shows, the ‘efficacy’ numbers are exactly the same no matter what the fixed rate is).
- Any vaccinated person who becomes infected within the first two weeks of his or her vaccination is classified as unvaccinated (in fact, as can be seen here, the Office for National Statistics classifies a person as infected within the first three weeks of his or her vaccination as unvaccinated. And also note this is the case in Sweden).
The Excel model can be downloaded from here.
Based on these assumptions, we find that a placebo is 86% ‘effective’ under a 14-day rule.
Here are the results shown in our new video.
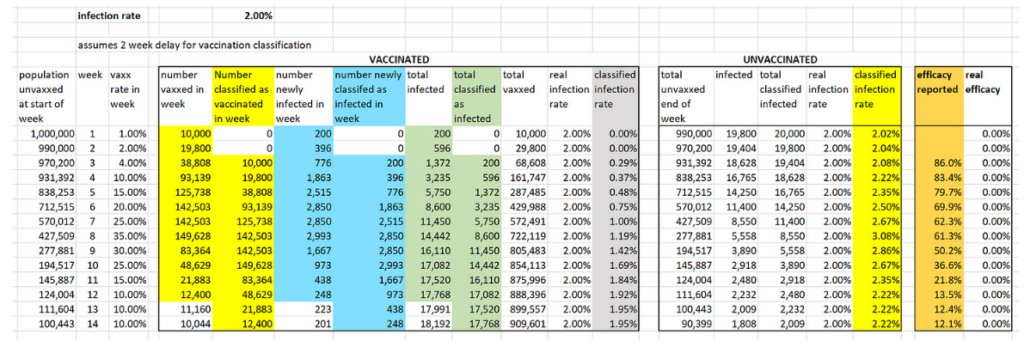
To calculate the infection rate for week n for those classified as vaccinated we divide the cumulative number of people classified as infected and vaccinated by week n by the cumulative number of people classified as vaccinated by end of week n.
For example, by end of week 4 a total of 161,147 people have been classified as vaccinated, of whom a total of 596 have been classified as infected. So the week 4 infection rate for the vaccinated is 596/161,147 which is 0.37%. We do the same for those classified as unvaccinated, so the week 4 infection rate for the unvaccinated is 2.22%. Note that, although the real weekly infection rates of the vaccinated and unvaccinated are always the same 2%, the infection rates after the ‘classification’ are always lower than 2% for those classified as ‘vaccinated’ and higher than 2% for those classified as ‘unvaccinated’.
To calculate the week n efficacy rate we divide the vaccinated infection rate by the unvaccinated infection rate and subtract this from 1, expressing the result as a percentage. Hence, the week 4 efficacy rate is 1 – (0.37÷2.22) = 0.834 = 83.4%.
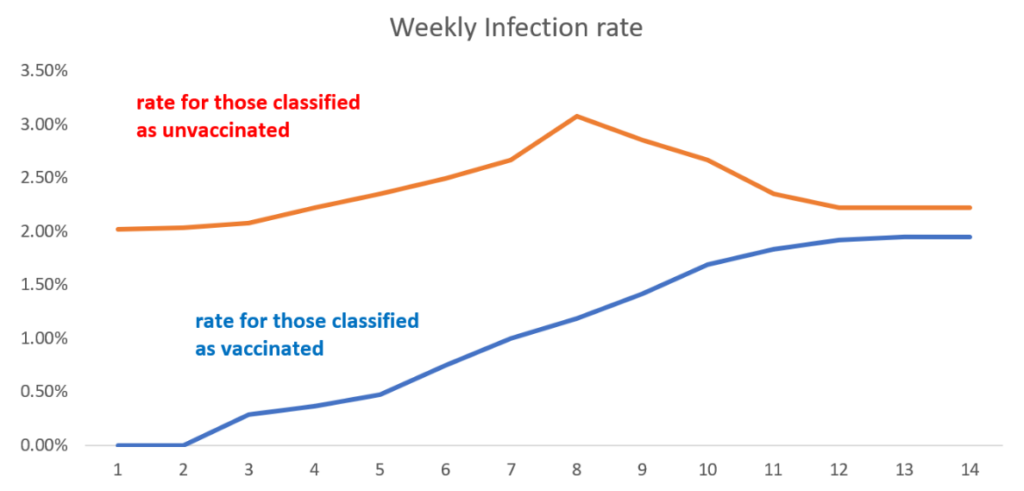
Now we see that a completely useless (with true efficacy 0%) vaccine appears to have very high efficacy in the first few weeks. Although it continually wanes it is still above 50% after week 9. By week 14 the efficacy is still positive but only 12.1% – hence the need for a new booster dose! These simulated results are very similar to the real-world efficacy rates that were observed in the first three months of a new vaccine or booster.
Here are the results if there is a three-week (21-day) period before a person is classified as vaccinated (as per ONS method).
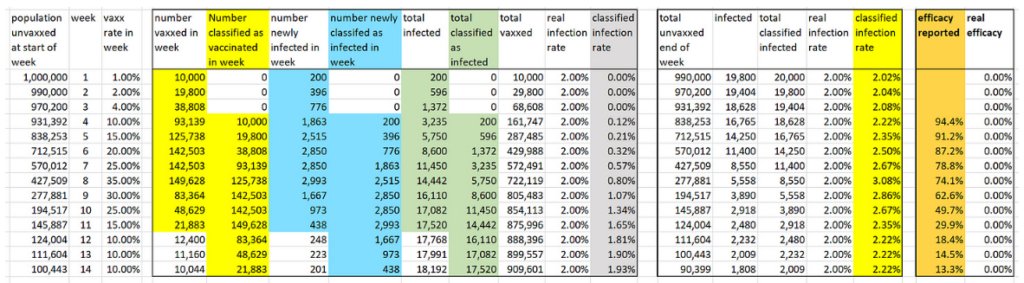
The efficacy achievable under the three-week (21-day) period is 95%.
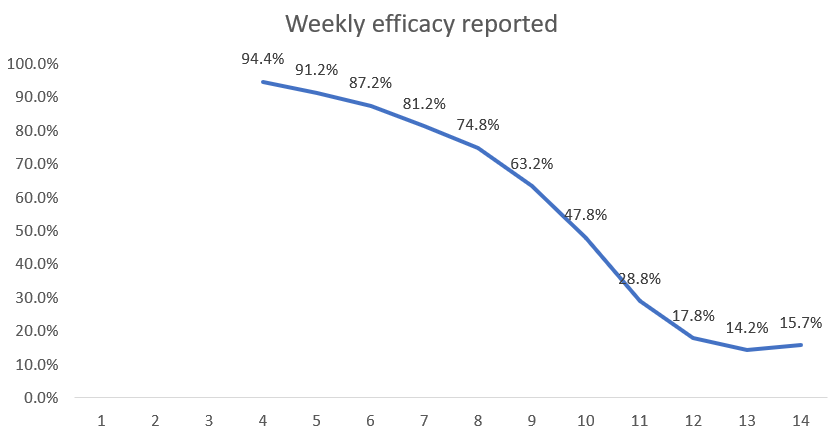
So now they could claim the vaccine starts with 95% efficacy, but again you need the booster after three months for vaccination to be truly effective.
For those who doubt the ONS calculates vaccine efficacy this way, here is a screenshot from its document.
The same applies for further doses where there is always a 21-day delay before being classified as having that latest booster shot.
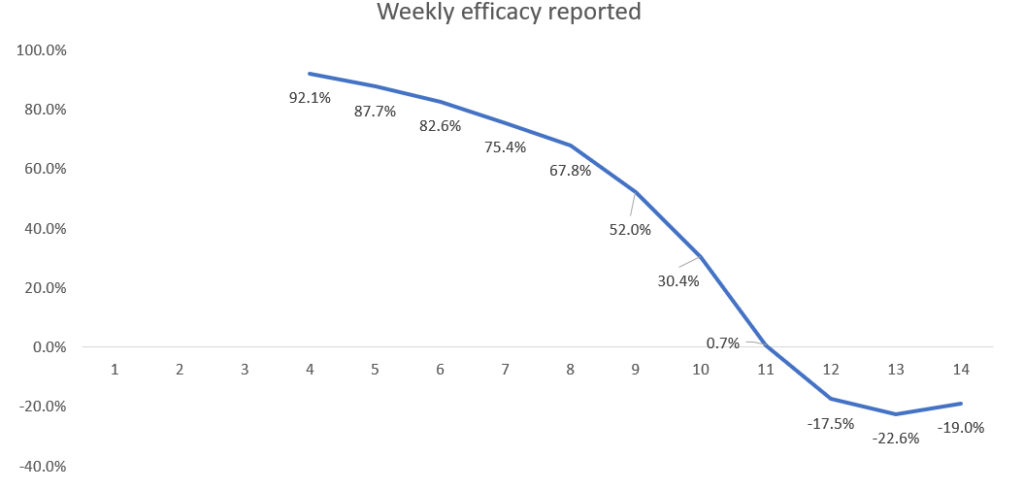
Even negative efficacy can be made to look 95% effective.
Note that for a placebo vaccine it is impossible to get negative efficacy. However, if there is a slightly higher infection rate for the vaccine compared to no vaccine then the same assumptions as above still yield high efficacy initially (92% at week 4) before eventually becoming negative. Here are the results if the vaccine actually increases the infection rate by 50% (so a 3% infection rate in the vaccinated rather than the assumed 2% in the above simulations).
Some caveats. In practice there are a number of factors which, if we included them in the simulation, would produce an even higher efficacy rate than could be claimed for a placebo vaccine. For example:
- The 2021 U.K. rollout happened during a period when the Covid infection rate was declining.
- Asymptomatic unvaccinated people were much more likely to be required to take PCR tests (to go to work or attend events, restaurants etc.) than asymptomatic vaccinated people, since the latter only had to show their proof of vaccination. In Israel during this period an unvaccinated person was six times more likely to have to be PCR tested than a vaccinated person. The high false positive rate for asymptomatics would therefore artificially increase the infection rate of the unvaccinated.
- People who were (or had recently been) PCR positive were not allowed to be vaccinated until 14 days after a negative test. This means the vaccinated cohort contained a higher proportion of people who already had natural immunity.
As we have shown the illusion of high efficacy is also present if the vaccine is worse than a placebo. In particular we know that, for the Covid vaccines, there was a disproportionately high infection rate within the first 14 days after vaccination. Given all of those infected within the first 14 days are classified as unvaccinated, this would lead to even higher efficacy rates than shown in our simulation.
On the issue of immunity, one simplification made in the simulation is that it does not take account of the fact that those who become infected during the period (whether vaccinated or not) would almost certainly not become infected again (and therefore should be removed from the count in subsequent weeks). However, unless the general infection rate is very high this has minimal impact on the efficacy results.
In conclusion, it may be reasonable to allow a certain amount of time for a vaccine to ‘work’. However, classifying a person who becomes infected within 14 or 21 days of vaccination as an ‘unvaccinated case’ in the calculation of vaccine efficacy is nothing short of a scam. It guarantees that any vaccine which is no different (or even worse) than a placebo will be seen to have high initial efficacy.
By using the 21-day period before considering a person vaccinated – as the ONS and others do for the Covid vaccines – means fraudulently high artificial efficacy rates are guaranteed. The apparent but completely artificial ‘waning’ of efficacy can also be used deviously to support the idea that after three or four months another dose of the vaccine is required to regain protection. Since the same delay in classification is used for those who have received a further dose, it is then guaranteed that high efficacy can again be claimed for the subsequent doses.
All of this creates a repeatable business model for Big Pharma.
Until he retired in January, Norman Fenton was Professor in Risk Information Management at Queen Mary University of London. Martin Neil is Professor in Computer Science and Statistics at Queen Mary University of London. This article first appeared on their Substack page, Where Are the Numbers?
To join in with the discussion please make a donation to The Daily Sceptic.
Profanity and abuse will be removed and may lead to a permanent ban.
Thanks for doing the sums. The conclusion that “All of this creates a repeatable business model for Big Pharma” could be true if they get away with the idea that a product is relatively harmless compared with the alternative, but not if the whole truth comes to light.
“Turtles All The Way Down” a new book, describes precisely how and why bigpharma conduct their clinical trials.
In a nutshell, just compare the safety and efficacy of the new improved product with the safety and efficacy of the previous one – which in turn was compared with – you’ve guessed it.
This model has been used for countless vaccines since the end of WW2.
Because Sars 2 and mRNA jabs were “new” bigpharma had no comparators so they resorted to shenanigans such as those revealed by Norma Fenton’s excellent work over the last few years.
You see, just the name of that book puts me off. It sounds ridiculous. Do you know why it’s called that? If it’s a reference to something then it’s lost on me.
It’s called that because of the infinite regression referred to by Sforzesca – each iteration of the vaccine is compared to a previous version of the vaccine rather than an inert placebo. The original reference is lost in time but is often associated with an anecdote about William James:
After a lecture on cosmology and the structure of the solar system, James was accosted by a little old lady.
“Your theory that the sun is the centre of the solar system, and the earth is a ball which rotates around it has a very convincing ring to it, Mr. James, but it’s wrong. I’ve got a better theory,” said the little old lady.
“And what is that, madam?” inquired James politely.
“That we live on a crust of earth which is on the back of a giant turtle.”
Not wishing to demolish this absurd little theory by bringing to bear the masses of scientific evidence he had at his command, James decided to gently dissuade his opponent by making her see some of the inadequacies of her position.
“If your theory is correct, madam,” he asked, “what does this turtle stand on?”
“You’re a very clever man, Mr. James, and that’s a very good question,” replied the little old lady, “but I have an answer to it. And it’s this: The first turtle stands on the back of a second, far larger, turtle, who stands directly under him.”
“But what does this second turtle stand on?” persisted James patiently.
To this, the little old lady crowed triumphantly,
“It’s no use, Mr. James—it’s turtles all the way down.”
Don’t let the title put you off – it is an excellent book and I would regard it as a must-read for anyone interested in the topic.
Thank you for the eloquence of your explanation of the Turtles. A strange title maybe but when you read it you’ll rapidly understand how apt it is.
If you weren’t a vaccine sceptic before, by God you will be when you’ve read it.
It really is very apt and the book is absolutely eye-opening. I’ve really been on a journey with vaccines over the last few years. I’ve had all the ones offered to me, as has my daughter, but I would make very different decisions now.
I read that when they conduct trials comparing drugs with their competitors they give higher doses of the competitors in the hope that more side effects will be produced with it.
I didn’t think the manufacturers had claimed that the “vaccines” were effective against infection, nor were they designed to be. They were meant to reduce the possibility of getting seriously ill or dying. Wasn’t it mainly governments that emphasised the infection aspect (which was implied by the “protecting others” lie and the rationale behind restrictions based on vaccination status)? I think also people assumed that the “vaccines” stopped infection because that’s what real vaccines actually do.
Bourla, head of Pfzier claimed it stopped infection. None of the phama companies did anything to refute the exaggerated claims.
I’m not doubting you but do you have a link for that? He must have “mis-spoken”. Yes indeed they were happy to go along with the lies and delusion.
April 2021 on Twitter …
Excited to share that updated analysis from our Phase 3 study with BioNTech also showed that our COVID-19 vaccine was 100% effective in preventing #COVID19 cases in South Africa. 100%!
Thanks for that.
“people assumed that the “vaccines” stopped infection because that’s what real vaccines actually do.”
I am such a committed sceptic these days tof that I take issue with the above, surely:
‘because that’s what we have been told real vaccines do.’
Yes that’s a very good point
Except vaccines do not stop infection, they train the immune system to fight the infection when/if it occurs so that serious or even noticeable symptoms do not develop.
An essential part of the PR campaign for the death jabs, the lying by omission, because if they’d only been billed as protecting from hospitalization and death then most of society wouldn’t have been ‘persuaded’ that they needed them because most of society were not at serious risk. Sticking exclusively with the elderly and others deemed ”vulnerable” would not have given half the profits Big Pharma have ended up with. Nor would only a fraction of society getting jabbed have facilitated the roll-out of the dreaded ”Vax Pass”. And so many high profile goons, such as world leaders, Fauci himself etc, publicly stating we wouldn’t get infected if we took the jab just helped the narrative and uptake along nicely for the entire network of criminals who were heavily invested in getting jabs into as many arms as humanly possible.
Coming up with a revised definition of a “vaccine” was also part of the scam. And now the WHO has redefined “pandemic”. What a surprise.
This entire article ( plus short video ) continually talks about ”prevention” and ”protection from” Covid. At no point do they make a distinction between ‘infection’ and ‘severe illness’. The jabs were always advertised to the public, deliberately, as a prophylactic intervention to stop people getting infected with Covid. Hence the emphasis on the high efficacy, which we know now went gradually down as time went by.
”Pfizer and BioNTech announced Monday their coronavirus vaccine was more than 90% effective in preventing Covid-19 among those without evidence of prior infection, hailing the development as “a great day for science and humanity.”
It means that protection from Covid-19 is achieved 28 days after the initial vaccination, which consists of a two-dose schedule. The final vaccine efficacy percentage may vary, however, as safety and additional data continue to be collected.”
https://www.cnbc.com/2020/11/09/covid-vaccine-pfizer-drug-is-more-than-90percent-effective-in-preventing-infection.html
Thanks
Yes, deliberately misleading
The absolute risk of symptomatic infection by the CoV 2 was shown in the Pfizer trial to be less than 1%. The risk after vaccination was less than 1%.
In other words, the vaccine (so-called) reduced a tiny risk to a tinier risk.
To ‘big it up’ they took the absolute risk of 0.88% and subtracted the risk ‘vaccinated’ of 0.04% to give a risk reduction of 0.84% et voilà the famous relative risk reduction of 95%.
By not mentioning that this was relative risk reduction, most people assumed that it would reduce disease in a vaccinated population by 95% in whom if unvaccinated disease would be 100%, whereas it would reduce risk by less than 1%.
Disease was only ever going to be 0.88% in an unvaccinated population. How severe the disease might be in an individual, vaccinated or not, would be entirely dependent on the condition of their immune system. There is no data on reduction of hospitalisations or deaths ‘thanks’ to the vaccine – just a lot of claims and assertions and anecdote.
Yes you’re right. A very effective and elaborate scam and the public were easily duped. The combo of the fraudulent claims about the pseudovaccines plus the intense and relentless PsyOp ( heavily enabled and amplified by the MSM ), ensured the vast majority of people were reeled in hook, line and sinker.
“claims and assertions and anecdote”. AKA “Lies”
To be honest, I’m not even sure they initially said the poison would even protect against serious illness or death, I don’t think those were end points in the original so-called trials.
It’s been a while, but I believe that at the very beginning the only thing that was actually claimed was that it would alleviate symptoms. I think the hope was then that if symptoms were not severe to start with, it would be unlikely for someone to fall seriously ill – not a completely unreasonable view in itself.
It then went to ‘it stops infection’ precisely because of the scam referred to above – it is not ‘nothing short of a scam’, it is and was an outright scam all along. Dollar signs and the opportunity to push the nazi pass took over at that point. The claims of preventing serious illness/death then started spreading to cover up the failure in preventing infection at a time when it was still necessary to con as many people as possible into getting/continuing to get stabbed. “No one ever said it would stop infection… – that’s not what vaccines do”
Yep.
https://www.bmj.com/content/371/bmj.m4037
The trials were not designed to prove either.
They were designed to prove that severe illness could be reduced to mild ones.
As that could neither be proven nor would have delivered a big sales pitch, they marketed first the bogus infection efficiency result and then the bogus death efficiency result.
https://www.bmj.com/content/371/bmj.m4037
That article from 2020 by Peter Doshi describes all that and also clearly states that transmission wasn’t investigated and why. In sofar, the infection efficiency = transmission efficiency perception, marketing and coercion was clearly stupid, evil and a lie.
That the world only woke up to it after the Pfizer executive’s admission in the EU hearing is therefore quite astonishing.
Doshi also wrote a good, sceptical initial review of the trials result delving into just that, so did Jon Rappaport.
I wonder why the Doshi article didn’t get a wider circulation back in October 2020. Anyone got any ideas??
The Pfizer phase 3 trial is here: https://clinicaltrials.gov/ct2/show/NCT04368728 None of its outcomes mention serious COVID. The only primary efficacy outcome measure was confirmed cases of COVID. The experimenters were allowed to be, and were, very selective in who they tested to confirm COVID. The “serious illness or death” public health message arrived quite late in the day, after the “stops infection” and “promotes herd immunity” messages had failed.
But lots of people, perhaps having the most recent public health messaging uppermost in their memory, do think that the clinical trials were about serious illness and death. The trials were nowhere near powered to measure those outcomes in what for most people is a fairly mild disease, so they would have failed if those had been the outcome measures.
The Pfizer clinical trial used to justify emergency use was designed to, and demonstrated, effectiveness at preventing symptomatic infection.
None of the subjects in either trial cohort had serious symptoms.
So yes the claim was effectiveness at preventing symptomatic infections and no, they made no claim about reduced severity of disease because that was not in the trial protocol.
Vaccines positively cannot prevent infections. They’re supposed to train the immune system to fight a specific kind of pathogen effectively without running the risk of getting sick because of an infection with it while still immunologically naive. In order for the immune system to do that (fight a pathogen) it must be there to begin with, ie, an infection must have occurred first.
The notion that infection, as determined by a PCR test, would actually mean something was/ is one the fundamental lies of the scamdemic. It doesn’t. Asymptomatically infected is the same as healthy or, to paraphrase Mike Yeadon, If your viral load is so low that it doesn’t cause symptoms, it’s not going to be high enough to infect others. It’s not possible to have high viral load without getting symptoms because symptoms of viral diseases are the effects of the damage the viruses inevitably causes to the host body by reproducing.
To whom it may concern in Government who reads what the “conspiracy theorists” are reading.
There must be someone in government reading these articles and these comments who can read this article objectively, do the maths, and come to either an agreement and urge the Government to be straightforward about this to the public to restore trust in the long term, albeit it won’t be easy in the short term to face the consequences
Or for that person to read it, do the maths and provide a resounding evidence based rebuttal. Please provide either.
They already know, they have known for a long time. Even giving them the benefit of the doubt that they really, truly wanted to believe the vaxx would provide the way out from their own humongous mistake of shutting down the entire economy for a cold virus, they had strong indications by March 2021 that the vaxx would not provide salvation, by April 2021 already had notice of serious AEs like myocarditis and by July 2021, when Israel was in another corona wave which was clearly hitting 2x vaxxed hard, it was clear that it was game over for the vaxx – except that at this point, they were all in – the time to come clean was summer 2021, but they decided to double-down.
Come clean now? As more and more studies show the damage caused by this garbage, as the pharma companies are seen for the profit whores they truly are rather than the saviours they were portrayed as, as the bullying, coercion and unlawful acts of the politicians become harder and harder to hide – they cannot come clean, they are too afraid of the consequences, and rightly so.
Great post.
Excellent work by Professor Norman Fenton! This is one of many misrepresentations by ONS.
Another is the bogus ‘ever vaccinated’ category that ONS quote here. It does not allow for cumulative effects of doses because each dose risk is based on a revised population, having removed victims of earlier doses. I would point people to Professor Fenton’s explanation of ‘survival bias’ that explains what is going on here.
There must be many people working at ONS who know that this skulduggery is going on. For goodness sake, speak up! You are perpetuating death and harms on your fellow citizens!
This is a stunning piece of work.
https://www.naturalnews.com/2023-05-02-ivermectin-as-effective-as-monoclonal-antibodies-against-covid.html
More info on the effectiveness of Ivermectin. As if more were needed.
Related to this on efficiency and Perseus on MHRA:
New info from a FOI request obtained by Judicial Watch about FDA and MHRA colluding to keep a side effect under wrap and Pfizer doing the same regards efficiency drop.
Seems the cardiologist cited by Andrew Bridgen will be proven right. Certainly, the criminal energy is there.
And so is Perseus with its assessment that the MHRA is unfit for (regulator) purpose.
They are doing very well as enabler.
https://articles.mercola.com/sites/articles/archive/2023/05/02/us-uk-hidden-pacts-to-hide-vaccine-reactions.aspx?cid_source=telegram&cid_medium=social&cid_content=mercola&cid=nonlead1_20230502
The scam was evident from the get-go, even to a layperson. All you had to do was look at the charts for Israel and the UK to see the infection rate shoot into the stratosphere as soon as the rollout began – the higher the climb, the more rapid the drop will be – all viral cycles ebb and flow. So yes, the claim of effectiveness was based on the inevitable end of the cycle, but the incredible jump in infections was clearly related to the jabs. I remember reading all the people commenting in the DM about how happy they were to have been stabbed, just so so unlucky that they happened to catch corona (having avoided it for almost 2 years), just in that 2-week period after being stabbed… nope, no pennies dropped.
An interesting comparison is to look at the vaxx rollout in NL. Whereas Israel and the UK went hell for leather to get needles stuck into any arm going within the shortest period of time, the Dutch rollout was very methodical by age group and went on for months. Compare the infection wave in NL from Jan. 2021 to May 2021 to that of the UK – it doesn’t have anything like the same peak, but remained high well into May – right along with the stab campaign, that did not get to those 50 and younger until the end of May/beginning June.
Also interesting is to note what happened beginning of July 2021. A big batch of J&J was about to expire, so then health minister De Jonge encouraged young people to go get it, so they could go on holiday and clubs could open up – no need to wait the 2 weeks before mingling. There was an extraordinary, short-lived spike in infections, with those in the ages of 15 – 30 having by far the greatest number of infections. The link between being stabbed and becoming infected within the first few weeks was there to see all along.
I’m convinced that’s why Big Pharma started so high with their claims of efficacy of their injections. It was purely tactics to encourage uptake. They knew prior to the jabs hitting the mass market that 90+% efficacy was an outright lie but they had to give themselves a decent margin in order to lower it as time went by and inevitably more “cases” were detected, the lack of efficacy becoming evident as people looked around and saw jabbed family, friends, colleagues still testing positive and getting ill. It gave Big Pharma time to adapt their narrative as the proof of their unsafe and ineffective products became more evident.
“Come and get your vaccine, with an efficacy of 50% protection against getting Covid. It’s our only way out of this deadly pandemic” doesn’t have quite the same positive and appealing ring to it. The efficacy had to be advertised as high in order to get high uptake from the outset. Who’s going to rock up for a crummy 50% efficacy novel technology jab with only 2 months of safety data? All a corrupt scam, as these data dumps that Pfizer wanted to hide from us for 75 years, and plenty of subsequent analysis from independent experts has revealed.
I don’t doubt Prof. Fenton’s findings as/but I won’t pretend to fully understand this approach for their effectiveness.
However, I, and anyone with an IQ above room temperature, have no difficulty at all understanding and concluding that any such 7/14/21 day misclassification is just a deliberate, egragious, evil and deadly fraudulent crime when applied to the assessment of their or any other drugs or vaccines safety.
And I do not even need to make a single calculation to see that.
Nor does anyone else, who has an IQ above room temperature.
I decided it was worth another £5 to pursue this one. It is an interesting point but surely any bias is removed by simply using the number vaccinated as of two weeks ago (or whatever the period is) as the population. Do we know that the various efficacy reports don’t do this?
I must admit that I initially thought the same but Norman Fenton covered this in an article some time ago. It’s not as simple as it seems…
Of much more importance though is that the rationale behind treating the vaxxed as unvaxxed for a 14 (or is it 21?) day period is that due to the vax the recipient is more likely to contract covid within that period and so for that reason, lol, they are deemed “unvaxxed”.
That may seem reasonable but the reality is that the vaxxed who get covid within that 14/21 day period enjoy the benefits afforded by natural immunity – thus handing a further unfair advantage to the vaxxed cohort.
Norman Fenton explains the above, and more, in the links referred to in this. Well worth following all his research and explanations.
I must admit that I initially thought the same but Norman Fenton covered this in an article some time ago. It’s not as simple as it seems
I can’t see where he addresses my point. The whole article seems like a rather lengthy way of making a good but relatively simple point.
Well done!
You would be crazy to assent to such treatment given that the understanding of the human organism is in its nascency.The work that is being carried out on the electro-magnetic relationship between cells along with the discovery of the interstitium and how this idea of a fluid organ within the body explains the proliferaton of cancer because that is how it was discovered. Just things like this should give you cause for concern. At the higher levels of healing there is an understanding that you have to heal one person who is often completely unrelated to another person you might heal. Like when Jesus went to heal the daughter of Jairus but healed someone else on the way there. These events are tied together.
It is clear that the ONS counts infected people as unvaccinated if they had the vaccine in the last 3 weeks (the numerator in the infection rate). What is not clear from the ONS screenshot is whether the total number of vaccinated people has been adjusted or not (the denominator). I.e., is the total vaccinated population equal to
those who have been vaccinated (including in the last 3 weeks)
or
those who have been vaccinated excluding anyone who had that vaccine in the last 3 weeks
The mirage of a difference in effectiveness disappears if you use the second definition.
Do we know for sure that the ONS applied the first definition?
Prof Fenton and his team stand out in this debate by explaining statistical illusions. We don’t need to know about viruses or vaccine development. All we need is a better understanding of statistics and nobody explains it better than Prof Fenton.
I have been spending time trying to get to grips with Fenton’s simulation. There seems to be something fundamentally wrong with it. The number of new infections among the vaccinated each week is only amongst those who have been vaccinated that week. But of course, given it’s a placebo, there will be infections amongst everyone who has been vaccinated to date. I am not sure how much difference it makes and I am reworking the spreadsheet to find out.
I reworked the Fenton spreadsheet with these changes:
The result is while you do get an artificial efficacy in the first 10 weeks or so this rapidly settles down so the infection rates for vaxx and unvaxx are almost identical. I will try to bring this to Professor Fenton’s attention.