Fall is coming and the Covid propaganda machine, fuelled by manufacturers of Covid vaccines, is already here. Without a single trial of the effectiveness against death, lipid nanoparticles that contain mRNA and perhaps more (remnant DNA?) will likely be added to regular flu vaccination every winter. Perhaps as soon as this winter they will no longer be called booster doses.
It is therefore an appropriate time to revisit the claims of high effectiveness of the first booster, which was added to the two-shot protocol two winters ago. Using empirical data from three sources, I will examine here what is left after accounting for the healthy vaccinee bias (to be explained) and show peculiar features of the data that indicate even deeper estimation problems. Then, I will discuss another bias, called differential misclassification, which cannot be easily removed.
Considering these two biases (there may be others), the true effectiveness of the first booster was somewhere between mediocre and zero, and it is impossible to narrow that range. Therefore, all those observational studies of the booster effectiveness were useless.
Taking a new Covid shot every winter, whether called booster or not, has no empirical basis. The burden of proving effectiveness against death squarely rests on public health officials, and anything short of a randomised trial is unacceptable.
The healthy vaccinee bias
I devoted several articles to this topic, which may be summarised as follows:
A naïve comparison of Covid mortality in vaccinated people and unvaccinated people, even if age-adjusted, is grossly misleading because the former have a lower risk of death to begin with. At least part of their lower Covid mortality, if not all, has nothing to do with the vaccine. They are simply healthier people than their unvaccinated counterparts. That’s called the healthy vaccinee bias.
Or vice versa: unvaccinated people are, on average, sicker than their vaccinated counterparts, and therefore have higher mortality in general, including mortality from Covid.
Biases have been studied extensively by epidemiologists, biostatisticians and others. But if you run a search for “healthy vaccinee bias” on PubMed, a well-known website for biomedical articles, you will not find many publications. There are only 24 (August 31st), including recent correspondence in the New England Journal of Medicine on the booster effectiveness.
The healthy vaccinee bias, which many mistakenly call selection bias, is a type of confounding bias. Moreover, it is not restricted to a comparison of vaccinated with unvaccinated but is carried forward with additional doses. Those who took the third dose were healthier, on average, than those who took only two doses. We’ll see the evidence shortly. Shifting of healthier people along the sequence of doses has another peculiar effect. For instance, the ‘leftover’ cohort of two-dose recipients becomes relatively sicker than (more comparable to) the cohort of unvaccinated.
The healthy vaccinee bias can be removed, at least partly, but little has been written on the method. As far as I know, two research groups independently developed a correction method for biased risk ratios: one group from Hungary; another from the U.S. Unaware of that work until recently, I also proposed a method. Interestingly, it turns out that it’s the same trivial maths, expressed in two or three forms.
Regardless of the maths, the common underlying principle is simple. We know that vaccinated people are healthier, on average. Let’s use data on non-Covid mortality to estimate their Covid mortality, had they been as unhealthy as their unvaccinated counterparts. In other words, we estimate the risk in a counterfactual state, which is not observable. Indeed, one of several ways to define confounding and deconfounding is based on counterfactual reasoning. (There are other ways.)
To correct the bias, we need data on non-Covid mortality by vaccination status. That type of data has been consistently hidden. So far I am aware of three sources of data on non-Covid death of recipients of the third dose: England, Wisconsin and Israel.
Data from the Office of National Statistics (ONS), England
The ONS is the largest of the three sources. That agency periodically publishes an extensive dataset with many levels of stratification, from which I extracted monthly data for those who received the third dose versus those who received only two doses. In both cases, I chose only those people who received the last dose at least 21 days ago, avoiding sparse data for some other categories and ensuring comparability. The time period I examined was November 2021 through April 2022, shortly after the initiation of the booster campaign till the next (fourth dose) campaign.
The ONS data include age-standardised mortality rates for all ages, and also rates for 10-year age groups with additional age-standardisation within those age groups. I chose the latter rates. The results were nearly identical using non-standardised rates, which is not surprising given the narrow age bands.
The example below shows that the rate of non-Covid mortality in the oldest recipients of only two doses was 2.19 times that rate in their age-matched counterparts who received three doses. Those who continued to take the booster were healthier on average. That’s the healthy vaccinee bias, which was present in every age group in every month. The ratio 2.19 is called the bias factor. Its value ranged from 2 to 5 in most of the ONS data I extracted. The lowest value was 1.7 and the highest was 8.1.
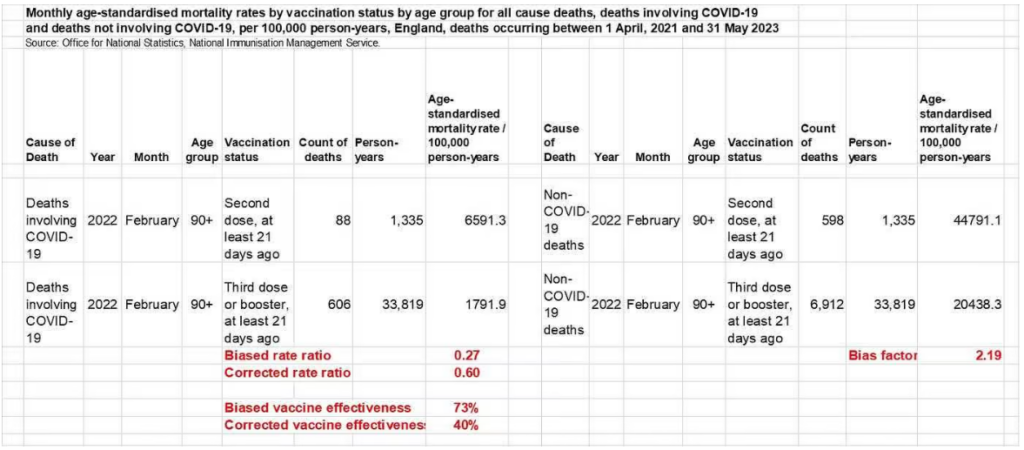
A naïve analysis produces a risk ratio for Covid death of 0.27 (vaccine effectiveness of 73%) attributed to taking a third dose versus taking only two doses. Both are biased estimates. To compute a corrected risk ratio we should multiply the biased risk ratio (0.27) by the bias factor (2.19), as explained elsewhere.
Rounding at the end of the computation, we get a corrected risk ratio of 0.60 (corrected vaccine effectiveness of only 40%).
A few methodological points:
First, as I noted earlier, the use of actual rates rather than standardised rates has made no material difference. The age groups were narrow enough. In the example above, we get exactly the same result whichever type of rate we use because the standardised rates were almost identical to the actual rates.
Second, when using actual rates, population denominators cancel out. Simple maths shows that we can get the corrected risk ratio by using only counts of deaths. I will skip the technical derivation and just show the computation for the example above:
Odds of Covid death (vs. non-Covid death) in third-dose recipients: 606 ÷ 6,912 = 0.088
Odds of Covid death (vs. non-Covid death) in two-dose recipients: 88 ÷ 598 = 0.147
Corrected risk ratio: 0.088 ÷ 0.147 = 0.60
Third, serious questions have been raised on the ONS denominators. However, this method of correction for the healthy vaccinee bias relies only on counts of deaths (which do matter a lot.) We will return to this topic at the end when I discuss another important bias: differential misclassification of the cause of death.
Fourth, sparse data (few deaths) is a common problem in estimation of vaccine effectiveness, especially when the sample is stratified. In the interval I analysed for the booster effect (November 2021-April 2022), it was not an issue. The ONS dataset is large enough to produce stable results at those levels of stratification.
Fifth, I restricted the computation to age 60 and above for two reasons: 1) the unbrainwashed reader knows that Covid has never been a public health issue for younger populations; 2) The number of Covid deaths in younger age groups was small.
The graph below shows a naïve analysis of the ONS data. The estimates of high effectiveness are useless for at least one reason: the healthy vaccinee bias. The ONS acknowledges the point, without using the word “bias.” It writes:
The ASMRs [age-standardised mortality rates] are not equivalent to measures of vaccine effectiveness; they account for differences in age structure and population size, but there may be other differences between the groups (particularly underlying health) that affect mortality rates.
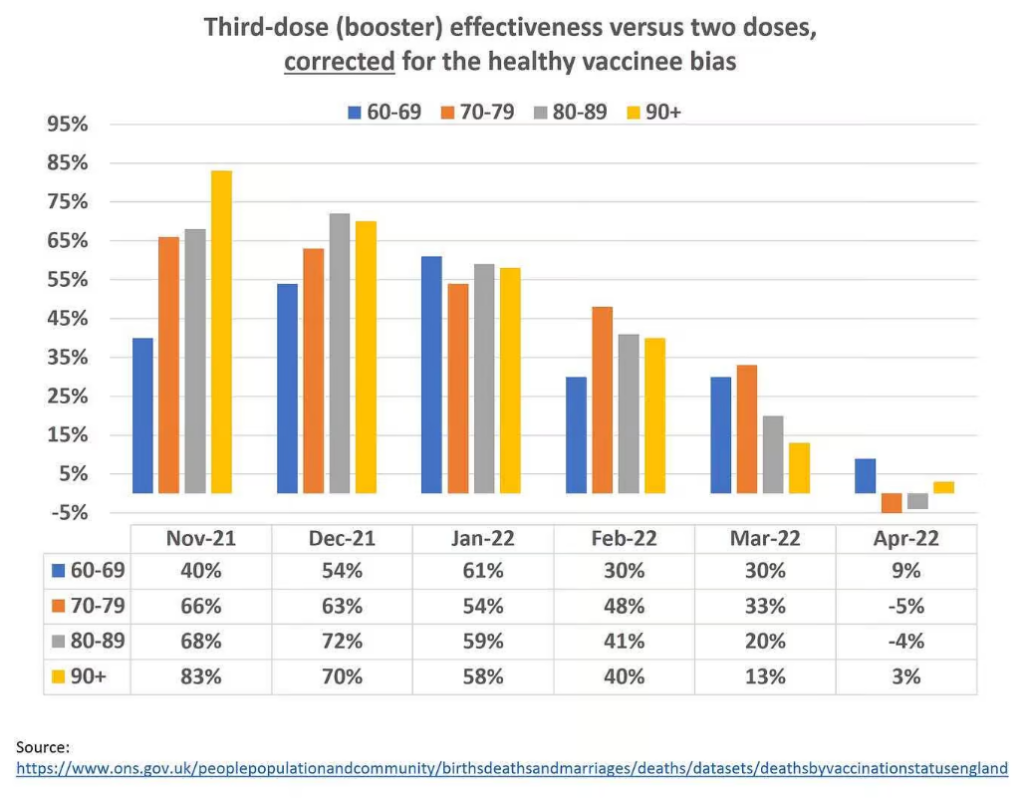
Corrected estimates of effectiveness are shown in the graph below. Comparing the second graph to the first, it is apparent that the magnitude of the healthy vaccinee bias was large, and in April 2022, biased estimates of 54% to 70% were essentially nullified. We also observe rapid and complete waning of effectiveness, which was not seen in the biased results.
Nonetheless, new questions arise after the correction:
- Why does effectiveness appear to increase with aging in many pairwise comparisons? For instance, why is it twice as high in the oldest than the youngest in November 2021? We expect to observe the opposite, given well-established knowledge from immunology.
- Why does effectiveness increase in the youngest age group between November 2021 and January 2022, and then rapidly decrease? Is there any biological explanation?
- Why is the linear, downward trend most consistent and sharp only in the oldest age group?
- Why are the estimates for the four age groups largely equalised by January 2022, and then diverge again?
Some features of the data simply don’t make sense. Why?
I offer the following answer to all these questions: either we did not remove the healthy vaccinee bias completely and uniformly, or some other bias-related processes have operated. Although we should confidently reject the original, biased estimates, we cannot endorse the new estimates as valid, final substitutes. They do not even qualify as upper boundaries of effectiveness. True effectiveness, if meaningful at all, should be much lower.
Data from Wisconsin
Data from Milwaukee County, Wisconsin is presented in a study by Yuan et al. (preprint) or Atanasov et al. (peer-reviewed version). Their article is among the best manuscripts I have read in my professional career, which does not mean that I agree with a statement such as “COVID-19 vaccines have saved millions of lives”. They did not. Nor do I agree with their claims about the benefits of the booster, as you will shortly see.
That article is exceptional on several counts: 1) independent discovery of the method to remove the healthy vaccinee bias; 2) thorough analyses at a level I have rarely seen (if you bother to read a lengthy appendix); 3) thoughtful discussions of almost every issue I could think about; 4) full exposition of the data. To my surprise, however, the phrase “healthy vaccinee bias” is never mentioned, nor is there any citation of previous work on the topic.
The authors have studied vaccine effectiveness of various doses against Covid death in residents of Milwaukee County, Wisconsin. From their overwhelming amount of data, I was able to extract and compute the numbers in the table below, which is essentially the same kind of data as the ONS data and the same kind of analysis — in two age groups rather than four, over three months (combined). Even after grouping, the data are sparse (a small number of Covid deaths).
As you can see, the results are peculiar. There was only moderate healthy vaccinee bias in ages 60-79 and no bias at all in ages 80-plus. What kind of healthy vaccinee bias was accounted for? Why do we observe a bias factor of 1? Following correction, the booster effectiveness in ages 80-plus was somewhat higher, not lower, than in ages 60-79. Are these the expected results?
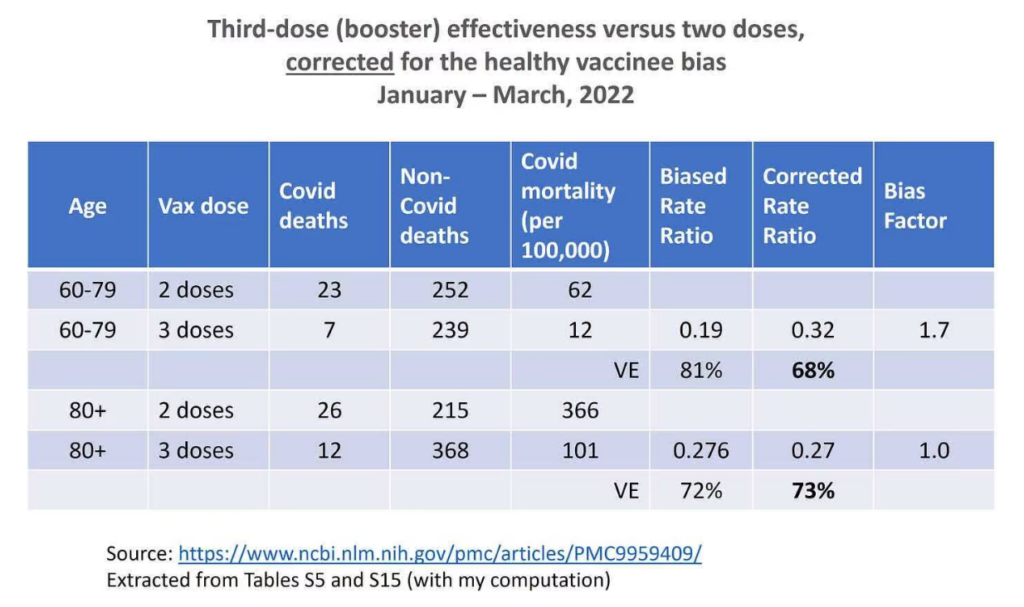
The authors write that “…selection effects, unless controlled for (through our CEMP measure or in another way), can produce large biases in VE estimates”. That’s correct, and we just saw it in the ONS analysis. But for some reason these effects did not seem to operate in their data for elderly booster recipients versus two-dose recipients.
I commend the authors for creative explanations of anomalous results (Appendix, pages 13-14). Apparently, no explanations were needed for the ONS data. The healthy vaccinee bias never vanished in any age group.
An excellent analysis cannot remedy problems that are inherent in the sample. It may be a sparse data problem alone or a lot more. Either way, we should have no trust in the new estimates.
Data from Israel
A letter to the editor of the New England Journal of Medicine has recently generated considerable interest in the healthy vaccinee bias. Høeg and colleagues astutely used data on non-Covid mortality from a study of booster recipients in Israel. In those data, biased vaccine effectiveness of 95% has turned into null after correction for the healthy vaccinee bias. The data are summarised below.
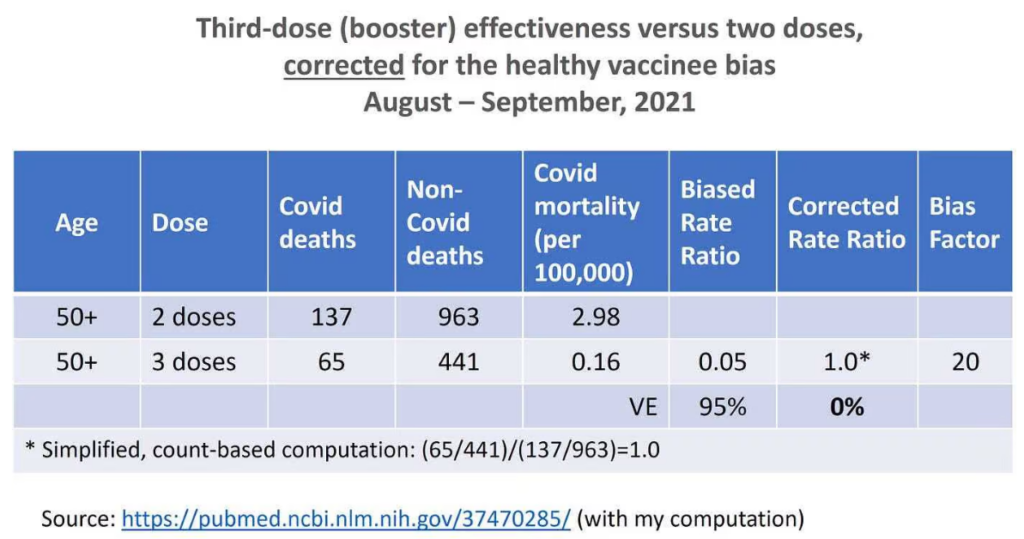
When a new method is introduced, new questions often arise, which are highly technical. Rather than correcting the bias using counts, rates or age-adjusted rates, it is also possible to correct the bias by a two-step procedure. First, we fit a multivariable regression model to remove as much confounding as we can, for both Covid death and non-Covid death. Then, we apply the counterfactual-based correction for the ‘leftover’ bias. The results may differ. For instance, in the study from Israel, the second method generated vaccine effectiveness of 57% rather than 0%.
- Are both methods valid, in the statistical sense of ‘unbiased results’?
- If so, which is preferred from a statistical perspective (say, smaller variance)?
The discussion is far too complicated to be included here. I will just say — for those with advanced statistical knowledge — that the two-step method is a hybrid of two approaches to deconfounding: classical conditioning and counterfactual reasoning. Whether that hybrid is justified, even if valid, is questionable. On the other hand, I am not aware yet of any overt pitfall of the single counterfactual approach, namely, the approach of Høeg et al., and mine.
Differential misclassification bias
Imagine two people who died in a hospital. Patient A received only two doses of a Covid vaccine; patient B received three doses (‘up to date’). Suppose Covid was the cause of death in both patients. Nonetheless, in our imperfect world there is misclassification, and one of the two deaths, or both, might be recorded as a non-Covid death. What kind of misclassification might be expected?
It depends on vaccination status.
We may assume that physicians are more reluctant to attribute death to Covid in a vaccinated patient than in an unvaccinated patient “because the vaccines are highly effective”. Still, they do record Covid as a cause of death in vaccinated patients, but they might do so differently for patient A (two doses) versus patient B (three doses). The Covid death of patient B, who is ‘up to date’ on vaccination status, is more likely to be mistakenly recorded as non-Covid than the Covid death of patient A who is not. By analogy, think about patient A as ‘unvaccinated’ and about patient B as vaccinated. Which Covid death is more likely to be missed? The latter.
The phenomenon is called differential misclassification bias, and I have no doubt that it was operating universally for various reasons: the mindset of physicians, PCR testing protocols, and so on. Nonetheless, it is difficult to quantify and remove the bias. When differential misclassification is added to the healthy vaccinee phenomenon, the bias is compounded. To illustrate the point, hypothetically, I used the sparse data from Milwaukee County, Wisconsin.
Suppose 5% of 491 non-Covid deaths in ages 60-79 were actually Covid deaths, which were misclassified (because physicians were convinced that the vaccines were highly effective and for other reasons). Nonetheless, there was differential misclassification as explained above: 6% of 239 non-Covid deaths in three-dose recipients (‘up to date’ vaccinated) were Covid deaths, whereas only 4% of 252 non-Covid deaths in two-dose recipients (‘unvaccinated’) were Covid deaths.
The computation is shown in the table below. After correcting for both differential misclassification bias and the healthy vaccinee bias, we get only 28% effectiveness of the third dose.
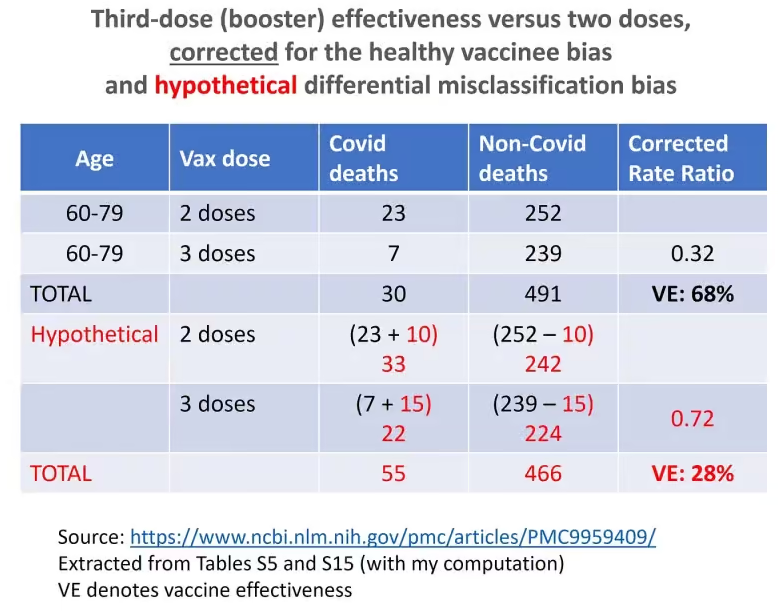
The authors of that study acknowledged that estimated effects would be biased if “the degree of undercounting differed systematically between vaccinated and unvaccinated persons”, but they “have no reason to expect that condition (ii) holds”.
As I wrote above, I do not share their belief. There are plenty of reasons to expect differential misclassification, and those of us who followed PCR testing practices in Israel, for example, have ample evidence.
I believe that some day, observational data on the effectiveness of Covid vaccines will be taught in epidemiology courses as prime examples of the healthy vaccinee bias, misclassification bias, other biases and other distortions.
To summarise:
The true effectiveness of the first booster was short-lived, if meaningful at all. Peak protection was somewhere between mediocre and zero, and it is impossible to narrow that range. Therefore, all those observational studies of the booster effectiveness were useless.
Taking a new Covid shot every winter has no empirical basis. The burden of proving effectiveness against death squarely rests on public health officials and anything short of a double-blind, placebo-controlled randomised trial is unacceptable. And that applies to the flu shot as well.
Dr. Eyal Shahar is Professor Emeritus of Public Health at the University of Arizona. This article first appeared on Medium.
To join in with the discussion please make a donation to The Daily Sceptic.
Profanity and abuse will be removed and may lead to a permanent ban.
Pre Crimes the Next Tyranny
8 days late? Perhaps the G has production problems; it would have made sense on 1/4, after all.
They should change the name once more to:
Sharing Archives To Improve Risk Evaluation.
The revised name comes with its own handy mnemonic.
The most scary bit here is acutally that our officials are stupid enough to believe this is possible. Especially, this includes being ignorant enough about pretty basic math to believe that the relative frequency of a non-random past even equals the probability of it repeating in future.
Despite being taught in GCSE Maths in the UK, the False Positive Paradox (aka Base Rate Paradox) still does not gel with most people, including ignorant officials. A highly relevant example of the paradox can be found by googling for “Base rate fallacy Example Terrorist identification”. (Ironically, Google’s AI introduction summarises this!)
The idea behind this is much more f***ed up. A probability is the relative frequency a specific outcome of a random selection will approach if the random selection is repeated often enough. The usual simple example is rolling a dice. Each individual outcome as a probabilty of ⅙ and this means there’ll be approximately n/6 occurences of each number when a dice has been rolled n times. The actual number of occurences will converge towards n/6 as n increases.
Relative frequencies can obviously be calculated whenever there’s a group whose members have a property X and a subgroup whose members also have an unrelated property y but the y/x is not the probability that the next person with property X will also have property Y as there’s nothing randomly selected here.
We don’t know what the outcome will be is a necessary condition for a random selection process but it’s not a sufficient condition: Just that we don’t know why something occurred doesn’t mean something occurred randomly.
Mathematical de-nonsenifying: Let nx be the number of people with property X and ny the number of these people with property y. ny/nx is know the relative frequency of number of people in the property X group which also have property Y but not the probability that the next person where property X is observed will also have property Y.
Good example – I like the example around tossing a coin – many people believe after a series of one result, you are more likely to get the opposite, when in reality it’s basically still 50/50 because each event is separate
This is actually not true because the probability of an event occuring is the number of times “event occurs” in the total set of events divided by the total number of events. When tossing a coin once, the total number of possible outcomes is 2 (front or back) and both front and back thus have a probability of 0.5 of occuring. But when tossing a coin twice, the total set of possible outcomes is
This means the individual probability of each outcome is now only 0.25. The number of possible outcomes doubles with each toss of the coin. But a sequence of all front or all back always remains only one of the possible outcomes. This means the probability of it decreases exponentially with the number of coin tosses.
Here we go again! Matt Hancock allegedly based his strategy to
control everyonecontain a ‘deadly, killer virus’ after watching the film ’Contagion’.Who has now been watching Tom Cruise in Minority Report?
Perhaps anyone that has should be subject to a double eyeball transplant without being told that it only works in the pretend world of Hollywood.
They’d need a brain transplant first
*For those who haven’t seen the film, Cruise plays a cop who, after being assessed by an AI pre-crime programme, is falsely accused of a pre-crime. He has to fight the system to clear his name.
Dear Mr Smith,
Our algorithms detect that you are more likely than average to commit murder, and so we need to talk to you about your thinking, and enrol you in our Homicide Awareness Course. You should report to Blogtown Community Centre next Monday at 6.30pm, bringing this letter and a utility bill with you as evidence of eligibility.
Failure to complete this course may make you liable to summary arrest in front of your children, 48 hours in our cells, and then release on Police Bail followed by a “no further action” notification, as is usual in non-crime situations.
If you belong to any of the following Protected Categories, you may ignore this letter…
I’m surprised that there is no mention of ‘number of years residing in the UK’ as one of the predictive variables.
So the algorithm might not work very well if they don’t include all the variables that correlate strongly with crime.
They can’t help themselves can they.
They’ve never seen a dystopian film or book without thinking “ooh that’s a good idea, we’ll try that”.
Truly we are governed by moral and intellectual pygmies.
“Explore alternative and innovative data science techniques…“
…Meaning find new ways of making stuff up. Outcome life sentence for the heinous pre-crime of predicted premeditated homicide.
Elementary, my dear Two-Tier.
Just another excuse to pry into private citizens and then control them. But it is all protect the individual. “Those who would give up essential Liberty, to purchase a little temporary Safety, deserve neither Liberty nor Safety.” Benjamin Franklin I believe.
Its been said before, but 1984 was not intended as an instruction manual.
“Statewatch says data from people not convicted of any criminal offence will be used as part of the project, including personal information about self-harm and details relating to domestic abuse. Officials strongly deny this, insisting only data about people with at least one criminal conviction has been used.” Like they denied the introduction of vaccine passports and look at what happened…..
This appears to be largely a re-run of the Home Office Initiative around 2001 (under various “Blair Babe” focus groups, presumably led by Jack Straw). This reached the level where the Home Office tried to get national and international definitions of mental illness changed to introduce a new one: “Severe and Dangerous Personality Disorder” (SDPD). This was defeated, not so much by human rights activists and lawyers, but by psychiatrists, doctors, medical professionals, researchers and, above all, mental health practitioners. On the whole these did not want the responsibility for “diagnosing” the politically-motivated new disorder of SDPD, especially as such a diagnosis would, under the Home Office proposals, render the person immediately liable to indefinite detention without charge, simply on the basis of a couple of opinions of psychiatrists. Also it tended to work the opposite way to that recommended by psychiatrists dealing with this type of case: namely, instead of encouraging the patient to take responsibility for their own actions, it would have specifically removed that responsibility from the patient and transferred it to the doctor, or the medical facility. As well as being psychiatric bad practice, it would have placed doctors and anybody else in a position of responsibility in a situation where they would be fearful of the consequences of NOT making such a diagnosis if the patient then went on to commit murder; such fear would tend to make the person adopt the contentious “precautionary principle” and make a SDPD diagnosis, knowing that they would not be held responsible for any violation of the patient’s human rights.
Twenty-five years later, what has changed? First, the government of the day still seeks votes by appearing to be able make the electorate “feel” safe from the extremely small number of people who pose a risk to the general public, while playing down the much larger risk of the much larger number of essentially basically harmless people, who happen to tick all the “right” boxes in the opinion of psychiatrists, being detained indefinitely. (It’s the old False Positive Paradox again, which came to fore during Covid testing.) Secondly, AI has come along, or whatever small development in software and hardware has been thus dubbed. This will encourage even more dependence on “computer says” diagnoses, based on even more obscure algorithms and models of human behaviour. The potential for unscrupulous, incompetent or merely mistaken people (whether entrepreneurial, medical, political, legal or social) to cash in on this, and the resulting human rights violations, will be enormous.
However, there will be opposition. One obvious tactic will be to point out that “psycho-eugenics” would be tainted by bad history, because it comes out of the same stable as eugenics, the difference being that eugenics was about extirpating carriers of “defective” genes, whereas psycho-eugenics is about extirpating carriers of “defective” memes. Another defence is the lessons from the psy-ops applied during Lockdown detecting people who might be labelled as potential “granny killers” just because they up-ticked a comment sceptical of the value of Lockdown and vaccination.
I hope this research does not result in the roll-out of an “early intervention” programme to stop crime before it occurs: the lessons of the 2001 Blair/Straw research must surely be available.
Scary!
“‘Murder Prediction’ Tool to Identify People Most Likely to Kill” Lite woke version no doubt.
The pre-crime tool will of course work only in identifying white people, any other person ethnic or sexual protected status will be filtered out.
I wonder if it could have predicted the Nottingham and Southport murders? It’s funny how all the layers of ‘experts’ couldn’t, yet the man on Clapham Omnibus would have done this in 5 secs.
This is just another boondoggle for the useless Home Office and MoJ.
At which university is this “research” taking place?
The Odeon or Cineworld.
Ha-ha! Brilliant!
Algorithm is:
white?
male?
not in trade union?
heterosexual?
not disabled?
score 2 or more positive answers to get arrested.
The biggest problem with this approach is not that it might identify those most likely to kill people but that following that identification nothing will be done.
Potential murderers will no doubt claim a right to enjoy a family life under the EHCR which trumps the ‘identification by algorithm’.
You don’t seriously want people to be punished for some AI claiming they might commit a crime in future with a certain probability, do you? If you do, why not just send people to prison street-wise? Some of them would certainly have committed some crimes otherwise! Or why not just gather people at random and shoot them?
Nice one. That’s a quote to remember:
“Why not just gather people at random and shoot them?”
Is this the real reason Stalin Starmer is so keen to force schoolchildren to watch that Marxist Indoctrination programme called “Adolescence”???
Softening up the public with propaganda, so they will accept White Working Class Boys as the primary targets of the “Pre-Crime Murder Prediction Tool”???
TPTB: We think you’re likely to commit murder so we have you under round-the-clock observation.
Subject: !! I’ll ****ing kill you. Make sure they get it on camera.
I presume this will only be deployed against white British people ….. since they know who the most likely to murder are and they all have various shades of darker skins and have come here from places where violence, particularly against women, is the norm and often sanctioned by their faith and their governments.
it was known at least thirty years ago that there are typically 39 to 39 antecedent criminal events prior to the major ‘index event’ such as murder, rape, etc and that the obvious job of the ‘relevant authorities’ was to work on the perpetrator during the first batch of criminal acts to prevent the probability of the major incident – but, as ever, the bureaucrats and politico’s ignored the research … no wonder we’re ‘at’ where we’re at