Detected fraudulence aside, there is no stronger criticism of a study than refuting the key result by using the study data. That opportunity does not arise often.
I present a striking example, pertaining to a study from Israel. Trying to be methodical, my article is somewhat on the long side, but the implications at the end are radical and broad.
Goldin et al. estimated the effectiveness of the Pfizer vaccine on several Covid-related outcomes, including death, in residents of long-term care facilities in Israel (mean age of 83 years). The large cohort (over 43,000) was heavily skewed towards vaccinated residents (90%). Only about 4,000 residents were not vaccinated.
Using a statistical method called survival analysis, the authors reported two age-adjusted values of vaccine effectiveness (VE) against Covid-related death:
- Skipping 10 days after the first dose, VE was 72%.
- Skipping about seven days after the second dose, VE was 85%.
Goldin et al. also analysed all-cause death as an endpoint, which many researchers have omitted. Most important, two of their figures (below) show the cumulative number of Covid deaths and all deaths at several time points — from which we can compute the cumulative number of non-Covid deaths. The latter data have been consistently hidden in studies of vaccine effectiveness.
Moreover, the studies provide mortality data, not just with the seven- or 10- day gaps, but since an ‘index date’ – the date on which the first dose was injected. We can thus analyse the data the way they should have been analysed – no skipping.
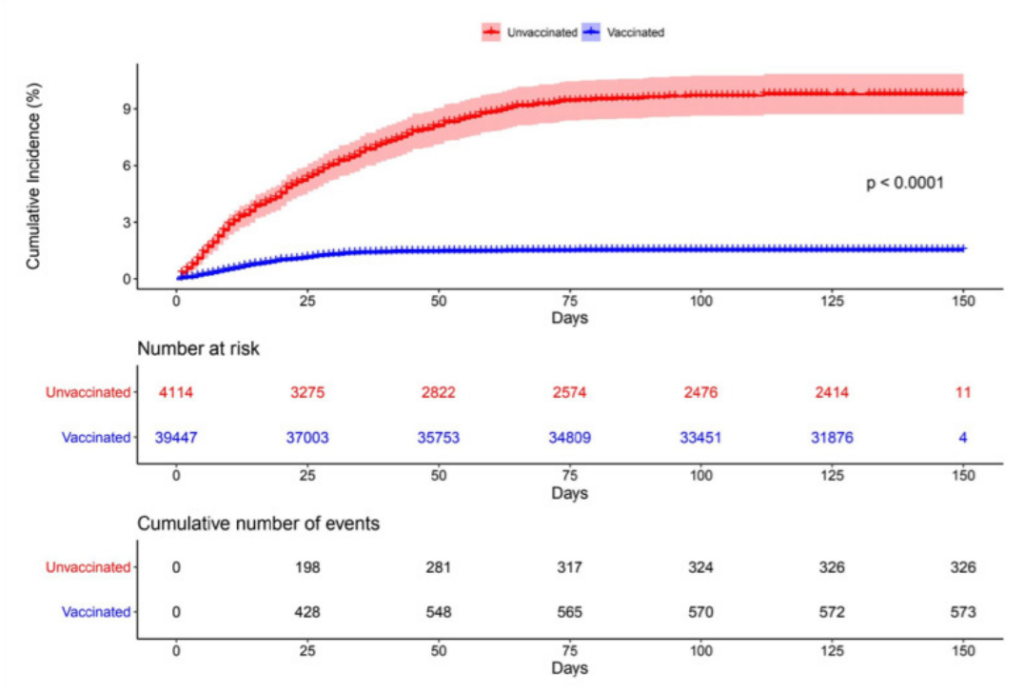
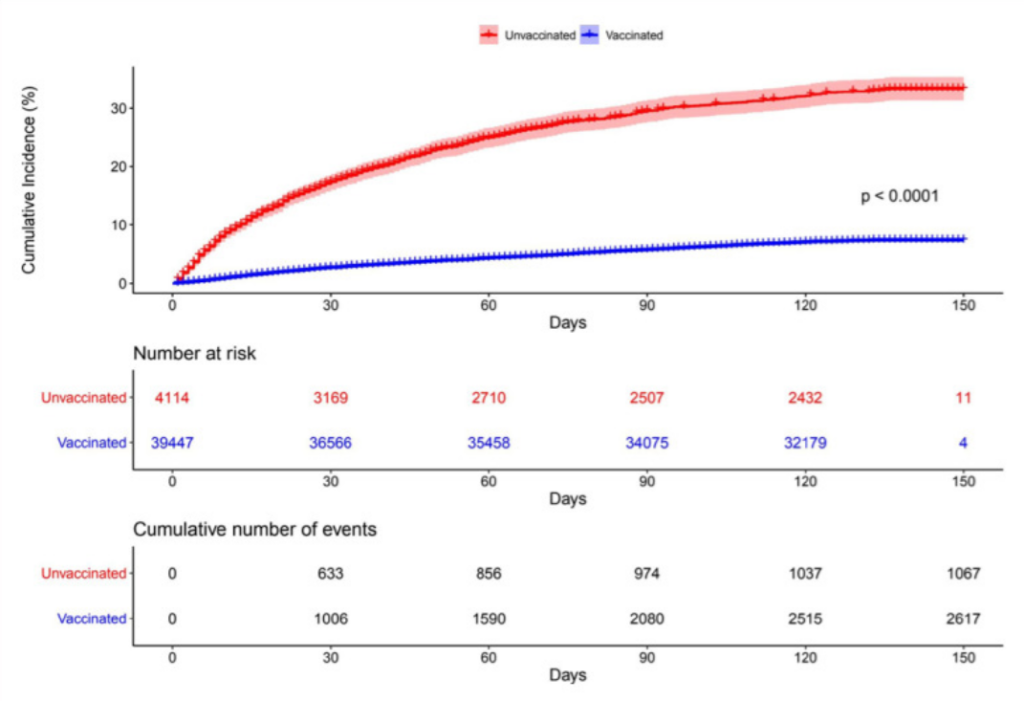
For some reason, the time points in the table for Covid death do not exactly match the time points for all deaths, but they are not too far apart (figures above). Therefore, the number of Covid deaths at the time points for all-cause death (30 days, 60 days, etc.) can be reasonably estimated by interpolation (examining the height of the line at 30 days etc.) Then, subtracting the number of Covid deaths from all-cause deaths reveals a crucial piece of data: the number of non-Covid deaths.
My busy tables below show the cumulative number of deaths (Covid, non-Covid) in vaccinated residents and unvaccinated residents by the end of the follow-up (five months) and by three interim time points (after one, two and three months). Using simple analysis, formally called ‘cumulative incidence’, I computed the risk of the two types of death in vaccinated (blue) and unvaccinated (red) residents.
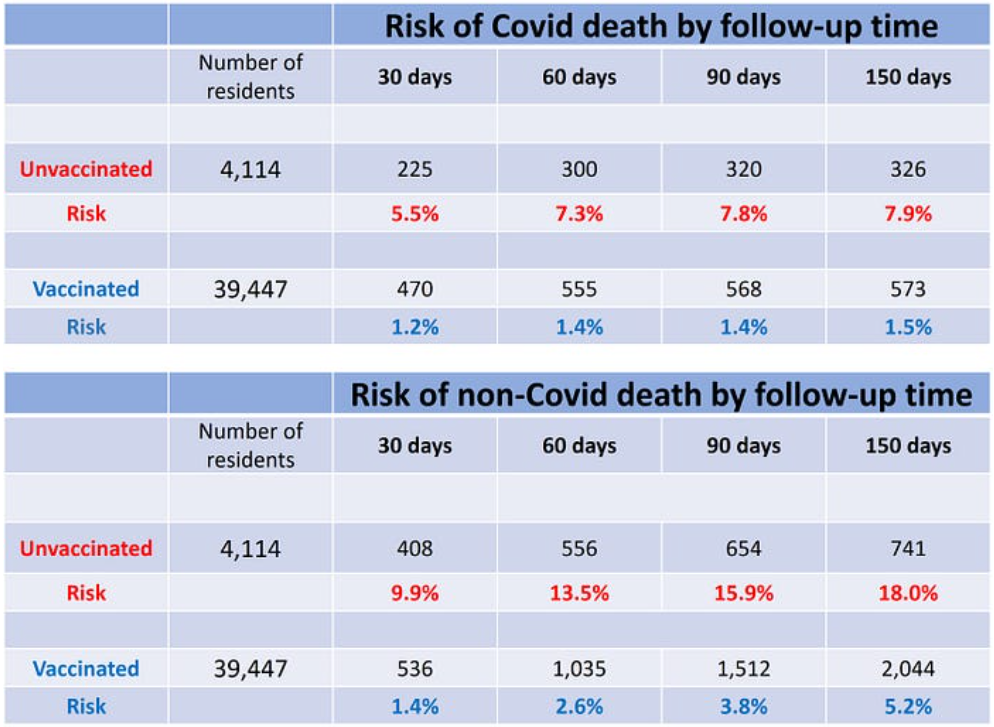
The top table shows that the risk of Covid death was consistently higher in unvaccinated than in vaccinated – a positive ‘vaccine effect’ – but the surprising result is revealed in the bottom table: that was also the case for non-Covid death! The mortality rate from non-Covid causes in 4,114 unvaccinated residents of nursing homes in Israel was three to seven times the mortality rate in their vaccinated counterparts, depending on the follow-up time. Or vice versa — the mortality rate from non-Covid causes was substantially lower in nursing home residents who were vaccinated against Covid. That astonishing result is seen early on, within one month of the first dose.
Does the Pfizer vaccine protect against death from non-Covid causes?
We have yet to hear someone making the claim.
If not, what is the explanation?
It is simple and not astonishing at all. The decision of whom not to vaccinate was not random. It must have been based on reasonable medical considerations, particularly life expectancy. For instance, what is the merit of vaccinating a 90-year-old who suffers from advanced dementia and metastatic cancer?
Those 4,114 unvaccinated residents were sicker to begin with. Their life expectancy was shorter, regardless of possible SARS-CoV-2 infection, and that’s why their non-Covid mortality was several fold higher.
Stated differently, belonging to the unvaccinated group was a general marker of poorer health. Or vice versa — belonging to the vaccinated group was a marker of better health. That’s on average, of course.
The phenomenon we observe here is called the ‘healthy vaccinee’ bias, and it is well documented in the research literature, dating back to flu vaccines. The bias is very strong in frail elderly residents of nursing homes, but it is seen in all age groups of the general population.
The implication of the ‘healthy vaccinee’ phenomenon — when estimating vaccine effectiveness — is called confounding bias. A naïve comparison of Covid mortality in vaccinated people and unvaccinated people, even if age-adjusted, is grossly misleading because the latter have higher risk of death to begin with. At least part of their higher Covid mortality, if not all, has nothing to do with not being vaccinated. They are simply sicker people.
Even Goldin et al. are aware of the bias, to which they devote one sentence at the very end of the article: “The unvaccinated group might have suffered from more comorbidities, leading them to be more susceptible to SARS-CoV-2 infection and death, thus making the vaccine’s effectiveness seem higher than it actually is.”
Some researchers think that the bias operates in the opposite direction (called confounding-by-indication bias), whereby the unhealthy person is more likely to be vaccinated because he or she is at risk. Regardless, the net effect of the healthy vaccinee bias and confounding-by-indication bias, if the latter exists, is shown in the bottom table (above): those who were vaccinated had substantially lower non-Covid mortality. They must have been healthier, on average, not the other way around.
The table below shows the risk ratio and VE against Covid death, as computed from the data in the top table above. VE is around 80% when calculated at various time points, and my simplified computation for the entire follow-up (82%) is similar to the main result of Goldin et al. (85%). Recall that all these estimates are distorted (biased) versions of the truth due to the healthy vaccinee bias (and naïvely assuming no additional sources of bias).
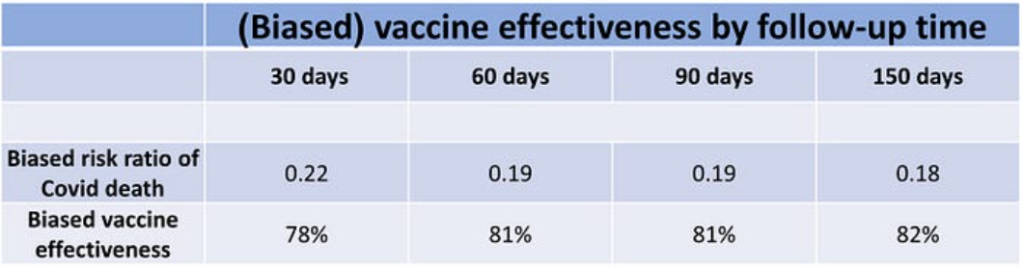
Most important, the data on the risk of non-Covid death allow for rudimentary correction of these estimates, which is certainly better than no correction at all. The method is best explained by a simple example.
Suppose the apparent risk of Covid death is twice as high in unvaccinated than in vaccinated, which means a biased risk ratio of 0.5 in favor of the vaccinated (i.e., the vaccinated are half as likely to die as the unvaccinated), and thus a biased VE of 50%. But suppose we find out that the risk of death from non-Covid causes is also twice as high in unvaccinated. What does that imply?
Vaccination has made no difference. It had no effect on Covid death. A two-fold risk of Covid death is the expected, ‘baseline’ risk of death in unvaccinated because they are generally sicker. Vaccinated or not, they would have had a two-fold risk of death from Covid than their vaccinated counterparts — just like their two-fold risk of death from non-Covid causes. The biased risk ratio of 0.5 (VE of 50%) should be corrected to 1 (VE of 0%).
To get a risk ratio of 1, from a biased risk ratio of 0.5, we need to multiply 0.5 by 2; the number 2 here may be called the bias factor. The bias factor captures the underlying higher risk of death in those who were not vaccinated; in the example, the unvaccinated were twice as likely to die of non-Covid causes, so the bias factor is 2. It is estimated by the calculating the risk ratio of non-Covid mortality, comparing the unvaccinated to their vaccinated counterparts.
In my simple example, the correction method completely nullified the presumed effect of a vaccine, the bias factor of 2 cancelling out entirely the biased VE estimate of 0.5. As we’ll see next, the outcome could be anything from attenuated VE to negative VE, where a supposedly beneficial vaccine is actually harmful.
The table below shows the bias factor in the study of Goldin et al. by follow-up time, along with the corrected risk ratio and the corrected VE. For example, over the entire follow-up, unvaccinated residents of nursing homes in Israel were 3.5 times more likely to die from non-Covid causes than vaccinated residents – a bias factor of 3.5. Multiplying the biased risk ratio of 0.18 (the risk ratio is 1 minus the VE, in this case 82%) by 3.5 changed the risk ratio to 0.63 and thus reduced VE from 82% to 37% (i.e., 1 minus 0.63, as a percentage).
Almost all Covid deaths have accumulated by the third month (888 out of 899). Indeed, the biased VE estimate was essentially the same (81% vs 82%). Since the bias factor was higher at 4.1 (because non-Covid deaths in the unvaccinated were higher earlier on in the follow-up), the corrected VE is now 22% (multiply the 0.19 biased risk ratio by 4.1).
Whether VE was 22% or 37% — that’s a mediocre vaccine. And worse results are forthcoming.
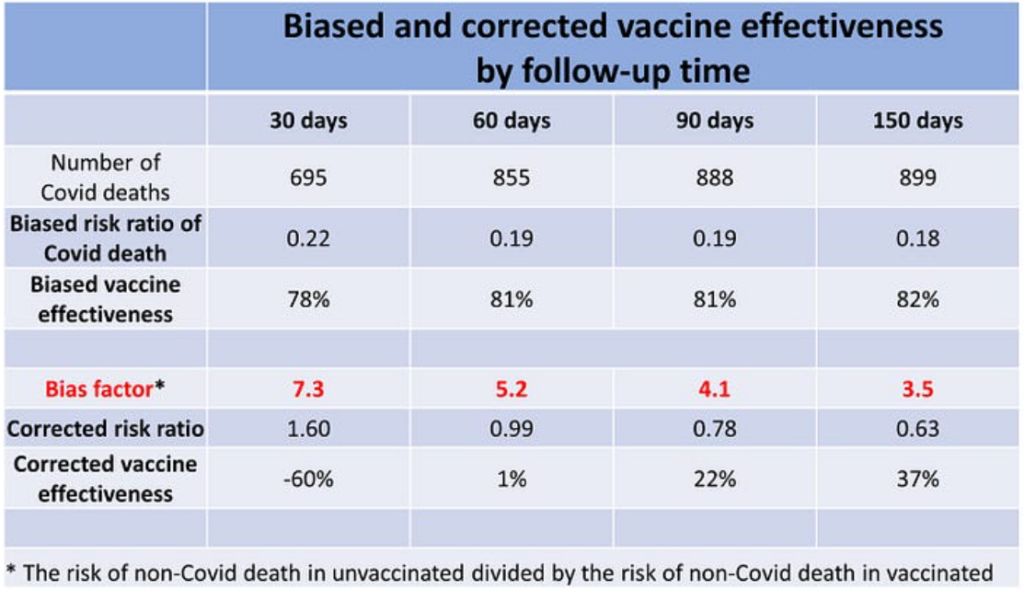
The biased estimates of VE increased slightly over time (from 78% to 82%). The bias factor, however, decreased from 7.3 in the first month of follow-up to 3.5 over the entire follow-up, which is not too difficult to explain. Given the shorter life expectancy of the unvaccinated cohort, the most vulnerable members of that cohort died earlier. The remaining people gradually made up a somewhat ‘healthier’ surviving cohort, thereby narrowing the non-Covid mortality gap between unvaccinated and vaccinated.
By the end of the first month the bias factor was 7.3 and by the end of the second month it was 5.2, whereas the biased risk ratio was similar in each month. This works out as a harmful effect of the Pfizer vaccine in the first month (VE of minus-60%), and overall null effect by the end of the second month (1% VE). That’s negative and negligible VE, respectively, against Covid death.
When, as in this case, the inference strongly depends on the amount of data accumulated — no effectiveness by the second month versus 22% and then 37% effectiveness with longer follow-up — researchers have a rule of thumb: the inference is stronger where we have most of the data, not after adding a few more observations. About 95% of all Covid deaths have occurred in the first two months (first row in the table above). This suggests the zero VE estimate may be the truest.
The correction method is not perfect, and the result depends on the value of the bias factor (an estimate by itself). Nonetheless, an increased risk of Covid death during an early post-vaccination hazard period is compatible with other data. Indeed, news outlets in Israel reported outbreaks of Covid infection in nursing homes shortly after the initiation of the vaccination campaign.
Below is a translated excerpt from a news report, dated January 14th 2021, about three weeks into the campaign:
Once again, a failure in nursing homes: at the same time as the second dose of COVID-19 vaccines is being distributed, the pandemic is hitting hard in the institutions where the elderly live. In the past two weeks, outbreaks have been recorded in no fewer than 160 geriatric institutions, and 1,098 new confirmed cases have been detected among residents of institutions licensed by the Ministry of Health alone.
In parallel to the surge in the number of patients in nursing homes and assisted living centres, in the past two weeks ‘Senior Shield’ [a task force for Covid management in nursing homes] stopped publishing the daily report on Covid morbidity data in geriatric institutions on the Ministry of Health website.
Why did they stop reporting? Have they also seen a surge in Covid death of vaccinated residents of nursing homes during the first month of the campaign?
Whether the Pfizer vaccine had time-dependent negative effectiveness, no effectiveness or mediocre effectiveness, the excellent effectiveness against Covid death of 85%, as reported by Goldin et al., was false. Assuming this conclusion is not challenged, what are the implications?
Some readers might think that refutation of one study does not mean a lot. Goldin and colleagues are wrong, but there are other studies that support the narrative of a ‘highly effective vaccine’ in the vulnerable population – and we did not show that the results from those studies were also false.
That’s not how deductive inference works. If VE against Covid death is shown to be far from ‘highly effective’ in one study of the frail elderly, we must deduce that all other studies that reported similar or better VE are false as well — likewise distorted by the healthy vaccinee bias. Otherwise, we have to make an implausible assumption: that despite the severe bias we have uncovered in Goldin et al., the play of chance nonetheless miraculously generated for the authors the true VE that matches other, non-biased studies. Far more likely is that those other studies, in producing a high VE, are similarly confounded by the healthy vaccinee bias.
What should happen next?
First, the paper by Goldin et al. should be retracted.
Second, vaccination of the frail elderly with updated Covid vaccines should be halted.
Third, public health agencies should initiate a Request for Applications (RFA) for placebo-controlled randomised trials of Covid vaccines in nursing homes — with Covid and all-cause mortality as endpoints.
Such trials are scientifically justified because residents of nursing homes, the most vulnerable population, were excluded from the original trials (in which death was not an endpoint). Moreover, randomised trials in this unique population become ethically obligatory when corrected VE against Covid death from observational data ranges from mediocre to negative and there are known vaccine-related fatalities.
Dr. Eyal Shahar is Professor Emeritus of Public Health at the University of Arizona. This article first appeared on Medium.










To join in with the discussion please make a donation to The Daily Sceptic.
Profanity and abuse will be removed and may lead to a permanent ban.
The author wrote ‘Whether VE was 22% or 37% — that’s a mediocre vaccine‘
Minus the dead and injured from the stabs and the VE is -ve 22 or -ve 37.
Even the flu quackcine has an ‘efficacy’ of 10-30%, after countless years of fake engineering and not accounting for people who get sick or worse from it (‘thank Lord Vaxx I was stabbed it would have….’)
The entire quackcine industry from rabies to Rona and all diseases in between is a scam. HIV for eg. is a $500 Billion market – drugs for a virus that does not exist.
Now that the Israelis are sure the quackery does not work, they can look at murders in the same old age home system with midazolam and morphine.
Yes, one flu vaccine left me very poorly – the Monday after the vaccine I got on the Tube and started to sweat… and sweat.. and sweat. By the time I got to work I looked like I’d run a marathon. I had to wring my cotton shirt out in the loo! I was tired for the better part of two years after. I’ve never been jabbed with anything since. All my faith in the medical industry beyond old-school ‘sawbones’ work has been shattered.
”Second, vaccination of the frail elderly with updated Covid vaccines should be halted.”
I’m at a point now, given all that I’ve learnt about vaccines generally, where I think elderly people should not be vaccinated with anything, period. We’ve all seen the evidence by now, such as the fraudulent sham that is the flu vax, for instance. These poor people, particularly the more advanced aged in care facilities, are just sitting ducks for Big Pharma. We are no longer living in cold, dirty, unsanitary slums where elderly people do not have even their most basic of needs taken care of and you will never acquire good health via a syringe.
What this demographic need is an emphasis on good nutrition/hydration ( often a challenge in elderly care ), with supplementation of Vit D, fish oils, get out in the fresh air and sunshine as often as possible and to have stimulation from being in a social environment, as contact with others is essential for mental health and wellbeing, even if that person cannot communicate their needs adequately. Just emphasise the basic things that humans have always needed to live optimally, which crappy pharmaceuticals will never be a substitute for.
And a low sugar diet with as little processed food as possible.
Totally agree – and not only is this more likely to prolong life than “vaccination”, but that life will have a better quality and surely quality of life has to count as a “public health” goal.
Neither safe nor effective, in other words. In line with the view of the HART Group here: https://www.hartgroup.org/did-injections-save-lives/
This is an understandable and plausible method and conclusion.
I have never been a big believer in the healthy vaccinee argument with regard to the general population, but (only) here it is surely very applicable and its effect very obvious.
Interesting to see though that the raw VE result calculated by the author is close to the ones obtained by the study’s author through skipping the deaths occurring shortly after a vaccination.
Again, that might/should be unique to these circumstances and be different when analysing the general population (s. Fenton).
Thank you Dr Shahar for highlighting this issue as few others, especially the MSM, seem willing to put their heads above the parapet to question vaccine/boosters for the elderly in care homes. My 88 year old Mother who had Alzheimer’s and had lost mental capacity died from the side effects of the Spring 2022 Moderna booster, as did another lady in her care home. I understand all the residents who received the booster became ill within 24 hours. I have been trying since August 2022 to get the MHRA to investigate the case but it has failed to do so, writing it off as coincidence because my Mother and her fellow residents were elderly and ill anyway. How can any reasonable person accept that mass ADRs within 24 hours of the Moderna and two deaths from those side effects do not constitute some sort of safety signal? How many other elderly deaths in close proximity to a COVID vaccine have been similarly dismissed outright as coincidence by the MHRA and therefore not investigated?
In my research these past few months I’ve been shocked to discover that clinical trial/safety evidence is missing for the use of Moderna in frail elderly with unstable health conditions and co-morbidities including chronic neurological disease. 70% of those in care homes in the UK have Dementia. Moderna’s Risk Management Plan highlighted the potential risk that such people may experience a different outcome from vaccination. The MHRA has failed to provide any safety evidence for giving multiple boosters to the over 75s in care homes in amongst COVID infection. COVID outbreaks in care homes still happen despite vaccination. Mum had COVID 4.5 months before the booster as did many other residents and I have since learned from various scientific studies that there seems to be a correlation between prior COVID infection and worse side effects from subsequent vaccination. The MHRA has also admitted it does not have safety data on all the various vaccine/booster permutations and that boosters have been rolled out to this vulnerable cohort ahead of such evidence.
The MHRA’s risk-benefit assessment for this cohort is focused solely on the risk to the individual of COVID-19 to the exclusion of all other risks and considerations. It has failed to heed the caution advised by the Norwegian Institute of Public Health after vaccine deaths in care homes in 2021 that “for those with the most severe frailty, even relatively mild vaccine side effects can have serious consequences”. My Mother’s death is a clear example of this. The Moderna caused vomiting and fever. Mum inhaled vomit and died from Aspiration Pneumonia which her hospital doctor told me is more dangerous than COVID. Vulnerable elderly who cannot look after themselves should not be given any drug that is highly likely to make them sick.
The JCVI, DHSC et al are not interested that the MHRA is failing to investigate cases such as this one and that their decisions for future boosters are therefore based on potentially significantly incomplete real world safety information. The one size fits all booster policy, the lack of information to enable informed consent, paying GPs by numbers to vaccinate care home residents, and care homes themselves requiring/preferring all residents (and visitors) to be fully vaccinated, all combine to act against the best interests of the individual.
Vulnerable elderly have died and will continue to die before their time because the MHRA is not doing its job. No-one with the power to ensure analysis of what is actually happening in care homes as a result of all the COVID vaccinations is bothering to do anything about it. Meanwhile my brother and I have to live with the fact that, in trying to protect her, our decision to allow Mum to have the booster led to her death. We would not wish that on anyone.
I hope that, in time, it will appear that your Mum and so many others like her did not die in vain, and that you and your brother find some peace.
Old people, even poorly old people, have a right to life too. Forget that and we’re done for as a society, even as simple functioning human beings.
Thank you TJN for your kind support, it means a lot. We lost Dad to end stage Dementia – his decline accelerated due to the social isolation of lockdowns – in October 2020, at home, in awful circumstances, and yes Midazolam was involved but I can’t go there. Sometimes the only thing that keeps me going is my campaign to get TPTB to wake up to the serious failings in pharmacovigilance and consequent policies. But after almost a year of battling the MHRA and contacting JCVI, Ministers, DHSC, my MP etc, I’ve got nowhere. My brother says that at least our concerns will be on record and hopefully one day the truth will out but that does not help other vulnerable elderly and their families who may not be aware, as we were not aware, of the risks from Moderna. I realise now the vaccine’s inherent side effect profile is wholly unsuitable for vulnerable elderly especially those who have lost mental capacity. To keep jabbing the vulnerable elderly without taking any account of this and their individual medical history, especially ref actual COVID infection, and on the basis of so little safety evidence, and without making the risks clear to people is immoral.
You are so right TJN to highlight that the elderly have a right to life too but as a society I fear we are in danger of forgetting that. The way the elderly have been treated since COVID started is a disgrace, whether in care homes, hospitals – though so many were denied access to treatment – and in their own homes. It boils down to a lack of respect and a lack of kindness and compassion. The elderly seem to be blamed for a raft of problems from overburdening the NHS because they are living longer and/or ill, to hogging houses too big for them, to Brexit and more. The promotion of so called ‘intergenerational unfairness’ by lobbyists and the MSM is poisoning relations between young and old. Maybe, in the interests of fairness, these lobbyists and their supporters would care to be bombed and machine gunned as Mum was during WW2, and endure years of rationing, and watch a young schoolfriend die of Tetanus because there were no antibiotics. It is facile to try and compare one generation with another. Mum used to say one can tell how civilised a country is by how it treats its most vulnerable. The answer is clear to me.
I thank the Daily Sceptic and similar for challenging the mainstream narrative and providing access to other views and evidence so that I can make up my own mind and stay sane. The comments posted by others make for enjoyable reading too! Wishing you all a great weekend!
There is one striking benefit of the pandemic, which is that published research has been subjected to rigorous analysis by real experts. I have peer-reviewed a large number of papers but am statistically undereducated, as I suspect are most clinicians. Nonetheless I have encountered many papers where even I have understood that the statistics are flawed, ranging from exclusion bias to use of the wrong tests. Articles such as this provide the necessary knowledge and show the extent to which papers require proper analysis before they are let loose. Systematic review of stuff recorded in the Daily Sceptic from coronavirus to climate science leads me to conclude that the one thing necessary in today’s research world is a fundamental change in the review system prior to any sort of publication.