by Dr. R.J. Booth

The apparent dwindling of Covid vaccines’ effectiveness at preventing infection has been disappointing, given that vaccines against some diseases last for many years or indeed for life. Nevertheless, the prospect of booster shots topping up immunity is a welcome one, which is promised by trials conducted by the drug companies. Still, it would be interesting to see whether there is statistical evidence that this is happening in the real world as third doses get rolled out. The executive summary is that I did find some good evidence, and it has encouraged me to book a third dose.
Dr. Will Jones has published articles on the Daily Sceptic which show unadjusted effectiveness rates of the vaccines, in comparison to unvaccinated people. These had worryingly strayed into significant negative territory until turning upwards more recently. But that work does not come supplied with a statistical test, and how much adjustment should be done to allow fair comparison of vaccinated and unvaccinated citizens is a fraught subject.
It occurred to me that since the third doses have been deployed at different rates in the different age groups, it might be possible to observe, and analyse, a ripple of decreasing infection rates from older to younger people over the last few weeks. So I developed a statistical model for infection rates, including a value dependent on the week (because the epidemic progresses at a rather unpredictable rate from week to week), and a week-dependent value proportional to the number of people who two or more weeks earlier had had the third dose compared with the number having had at least the first dose. I divided out the infection rate data by its value in the first week, to put the different age ranges on the same footing.
Mathematically, the model is written as:
r(a,w) = c + b(w) + z(w) d(a,w) + error (1)
Where a is the age group, w is the week number, r is the infection rate relative to the first week, b is a week-dependent adjustment, d is the proportion of third doses, and z is a week-dependent multiplier to d. The values r and d are deducible from public data, and the values b and z need to be inferred from the data and the equation. A technique called linear regression allows this to be done by minimising the sum of the squares of all the errors.
Technical note for the keen reader: It might be thought that a more logical equation would apply separate effects to two-dose people and three-dose people, like r(a,w)=c+B(w)+Y(w)(1-d(a,w))+Z(w)d(a,w) plus error – (2). However, dropping the (a,w) parameters, this can be written as r=c+(B+Y)+(Z-Y)d, which is of the same form as Equation (1) with b=B+Y, z=Z-Y. Because any x could be added to Y and Z and subtracted from B without altering the result, Y, Z, and B cannot be uniquely determined, whereas z and b can, providing that d(a,w) has some variation with a. The ratio of interest to compare two dosers with three dosers each week is f = (c+B+Y)/(c+B+Z) = (c+b)/(c+b+z) – (3).
What we would hope to see would be that the best estimate for z(w) would be negative, indicating that a higher proportion of third doses leads to fewer infections, especially in later weeks when d(a,w) is higher. This makes the factor f in favour of three dosers greater than one in Equation (3) above.
For data, there are two resources: the NHS Covid Vaccination Archive, for vaccination data, d(a,w), and the Government’s Covid vaccine weekly surveillance reports for four week infection rate data, one of them kindly supplied by Will. The one week relative infection rates r(a,w) are deduced from the four week rates by fitting a straight line through five weeks and then taking differences. This process could add to errors in the model, and it would be better if raw one-week infection rates could be obtained.
| age\week | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| 50-59: r | 1.00 | 1.12 | 1.24 | 0.97 | 1.01 | 1.06 | 1.19 | 1.21 |
| d | 0.02 | 0.03 | 0.05 | 0.07 | 0.09 | 0.11 | 0.14 | 0.20 |
| 60-69: r | 1.00 | 1.18 | 1.35 | 1.04 | 1.06 | 0.98 | 0.99 | 0.77 |
| d | 0.02 | 0.02 | 0.04 | 0.07 | 0.11 | 0.17 | 0.25 | 0.38 |
| 70-79: r | 1.00 | 1.15 | 1.31 | 0.77 | 0.62 | 0.44 | 0.55 | 0.27 |
| d | 0.03 | 0.05 | 0.12 | 0.22 | 0.36 | 0.49 | 0.64 | 0.75 |
| 80+: r | 1.00 | 1.10 | 1.21 | 0.46 | 0.58 | 0.56 | 0.73 | 0.29 |
| d | 0.13 | 0.20 | 0.34 | 0.47 | 0.58 | 0.66 | 0.72 | 0.77 |
In Table 1, for each age group, the first row is r(a,w) from Equation (1) and the second row is d(a,w). A linear regression for this equation was performed across all age groups and weeks, and the results are in Table 2.
| Variable | Estimate | +/- in Estimate | Significance |
| c | 1.00 | 0.06 | <10-10 |
| b(42) | 0.16 | 0.08 | 5.5% |
| b(43) | 0.32 | 0.08 | 0.1% |
| b(44) | 0.09 | 0.08 | NS |
| b(45) | 0.11 | 0.09 | NS |
| b(46) | 0.14 | 0.09 | NS |
| b(47) | 0.26 | 0.10 | 1.9% |
| b(48) | 0.46 | 0.11 | <0.1% |
| z(42) | -0.31 | 0.61 | NS |
| z(43) | -0.31 | 0.37 | NS |
| z(44) | -1.37 | 0.27 | <0.1% |
| z(45) | -1.02 | 0.22 | <0.1% |
| z(46) | -1.06 | 0.20 | <10-4 |
| z(47) | -0.91 | 0.18 | <10-4 |
| z(48) | -1.57 | 0.18 | <10-6 |
The error term in Equation (1) has an estimated mean of zero (by design) and a standard deviation of 0.09. The notable results are as follows:
- Weeks 43, 47, and 48 had significantly higher new infection rates than week 41
- Weeks 42 and 43 showed a third dose benefit but not to a significant level
- Weeks 44 (November 1st-7th) to 48 all showed significant benefits from third doses
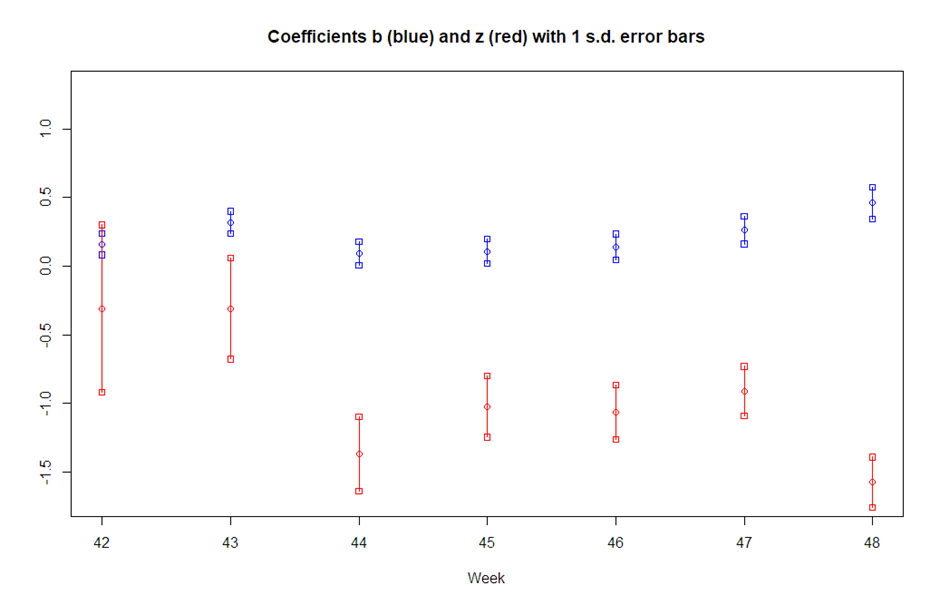
It should also be noted that the ‘true’ values of c+b+z, roughly 1+b+z, being relative infection rates for three dosers, must be non-negative, which precludes the lower ranges of b and z being valid in some cases, and this is especially true of weeks 44 and 48. It is therefore not an easy task to give a sensible estimate of the factor (equation (3)) for the advantage of three dosers over two dosers. But clearly, where the mean of the estimate c+b+z is negative, this factor is likely to be substantial.
I conclude that though three doses of vaccines may have been effective from the outset, statistical support for that proposition via these sources did not become apparent until week 44’s data was published, when nearly half of over 80’s had had boosters two or more weeks earlier, but has been sustained since then. Of course, ‘statistical support’ is not a cast-iron proof, as correlation is not causation and there might be ‘unknown unknowns’ at work. Nevertheless it is highly suggestive that the prior statistical work on Covid vaccines is vindicated here.
It is satisfying to have shown the benefit of third doses without having data on actual infection rates occurring in people with three doses, but if such data become available then the benefit may prove to have occurred earlier than week 44.
UPDATE (1/1/22):
Soon after this article was posted, a commenter called ‘confounder’ proposed a challenge for me (the comment can be found by searching for “highly flawed”). The challenge was to use my model to make a testable prediction for week 1 of 2022.
He/she also made their own prediction: “I predict by early January 2022 the majority of those dying following a positive Covid test will be triple dosed. By mid Feb I am willing to call more than 75% dead with positive test result triple dosed.” Now that prediction isn’t particularly controversial, because most people who die of COVID-19 are old, and an ever increasing proportion of old people are getting triple dosed, so it would take very high vaccine effectiveness against death for unvaccinated deaths to predominate.
I am generally sympathetic to suggestions that statistical models should be used to make testable predictions, but there are two difficulties with the request by ‘confounder’. The first is that my article was about case rates, not deaths. The second is that the very nature of my model is to be forensic rather than predictive. Confining attention to case rates, recall that my model is:
r(a,w) = c + b(w) + z(w) d(a,w) + e(a,w)
where a is the age group, w is the week number, r is the infection rate relative to the first week, b is a week-dependent adjustment, d is the proportion of third doses at least two weeks prior, z is a week-dependent multiplier to d, and e is an error term (assumed to have a normal distribution).
Because the output r(a,w) depends on the weekly parameters b(w) and z(w) to reflect changes which might be hard to forecast, these values need to be guessed in advance to make a prediction. (The same is true of d(a,w), but the two-week lead time for that helps to make it available in time.)
Here are the details on when information usually becomes available. The 2022 Week 2 COVID-19 vaccine surveillance report, which will cover four-week rates to January 9th at the end of 2022 Week 1, should be published on January 13th. The relevant COVID-19 Vaccinations Archive report is the one covering the end of 2021 Week 51, namely December 27th, and that should be available on about January 3rd.
Before predicting Week 1, I decided to start with an easier task, namely to predict Weeks 49 and 50 (of 2021) before their data were available. Extrapolating my graph by eye, I chose b(49) = 0.50, z(49) = -1.20, b(50) = 0.55, z(50) = -1.25. Here are the results, where the E columns are for the estimates/predictions, and the O columns are for the observed values subsequently retrieved from the internet. The published standard deviations (±) of my estimates have contributions from standard deviations observed in e and in the estimates of b and z.
| age\week | 49E | 49O | 50E | 50O |
| 50-59: r | 1.18±0.16 | 1.10 | 1.09±0.17 | 1.83 |
| d | 0.27 | 0.37 | ||
| 60-69: r | 0.89±0.18 | 0.72 | 0.76±0.19 | 1.29 |
| d | 0.51 | 0.63 | ||
| 70-79: r | 0.52±0.21 | 0.36 | 0.48±0.22 | 0.78 |
| d | 0.82 | 0.86 | ||
| 80+: r | 0.54±0.21 | 0.50 | 0.51±0.21 | 0.95 |
| d | 0.80 | 0.83 |
Note that my Week 49 estimates were quite good, with all four being within one standard deviation, but my Week 50 estimates were rather bad. The reason for that is, of course, Omicron. There were other data on that which I ignored, that implied that it was rising rapidly. So I do not, after all, feel inclined to predict Week 1 relative infection rates!
When I actually fit Week 50 data (and no other weeks) to my model, I get b(50) = 2.58 and z(50) = -2.04, very far from my guesses of 0.55 and -1.25. The important thing, though, is that the significance level for z(50) proved to be just 0.2%.
In the main article I wrote that it is “not an easy task to give a sensible estimate of the factor [say f] for the advantage of three-dosers over two-dosers”. I have now done something on this. (Technical note: from b and z I created two “orthogonal” variables u and v whose estimated values would have independent t-distributions on two degrees of freedom, and I integrated over the probability distribution of one of them and multiplied that by the tail probability of the other, to get a probability that the desired factor f was less than x; by varying x I found fp such that P[f < fp] = 100p.)
The table below has significance levels for z in all the weeks 42 to 50, and also the median f50 and 90% confidence interval f5 to f95. (The p-values for z differ from Table 2 above because here there is a separate regression for each week; this allows some weeks to have a higher estimated error variance than in the combined regression, and that has a knock-on effect on the significance levels.)
| Week | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| z p-val | 0.130 | 0.164 | 0.004 | 0.030 | 0.045 | 0.040 | 0.006 | 0.010 | 0.002 |
| f5 | <1 | <1 | 53.7 | 1.4 | 1.1 | 1.1 | 7.2 | 2.8 | 3.3 |
| f50 | 1.3 | 1.3 | >100 | 12.7 | 14.4 | 3.6 | >100 | 7.5 | 4.7 |
| f95 | 3.9 | 3.6 | >100 | >100 | >100 | >100 | >100 | >100 | 7.5 |
The p-value for z remains extremely low, indicating that either the third vaccine dose has a beneficial effect or there is something else at work. If it is the vaccine then the ranges from f5 to f95 show that the magnitude of the effect cannot be pinned down from these four age ranges, but a median value of five is not implausible.
‘confounder’ does raise the question of alternative explanations, such as “people who think they have a triple dose covid forcefield are initially less likely to get tested until they realise the forcefield is not as good as they thought”. However, those confident people might also be more likely to socialise and perhaps ignore distancing directives, and so be at greater risk of getting symptomatic Covid, which would spoil the figures we see. Or, being generally older, they might be less confident, with probably less risk of infection, and in that case some of the apparent vaccine effect would be explained that way.
My model may become less useful in the future. For, when (if) the third dose rate in the 50-59 group reaches 80%, it is unlikely that the dose differential will be sufficient to give significant z(w) values. This will not mean that the third dose had stopped working, merely that its effect would be undetectable with this method unless the age groups were extended.
Dr. Richard J. Booth is a retired civil servant with a Ph.D. in mathematical statistics.










Donate
We depend on your donations to keep this site going. Please give what you can.
Donate TodayComment on this Article
You’ll need to set up an account to comment if you don’t already have one. We ask for a minimum donation of £5 if you'd like to make a comment or post in our Forums.
Sign Up2021 Was an Outstanding Year For Eco Crackpots And Hypocrites
Next PostNews Round-Up